11 KiB
计数排序
如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 tan45du_one ,备注 github + 题目 + 问题 向我反馈
感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
另外希望手机阅读的同学可以来我的 公众号:袁厨的算法小屋 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击刷题小队进入。
今天我们就一起来看看线性排序里的计数排序到底是怎么回事吧。
我们将镜头切到袁记菜馆
因为今年袁记菜馆的效益不错,所以袁厨就想给员工发些小福利,让小二根据员工工龄进行排序,但是菜馆共有 100000 名员工,菜馆开业 10 年,员工工龄从 0 - 10 不等。看来这真是一个艰巨的任务啊。
当然我们可以借助之前说过的 归并排序 和 快速排序解决,但是我们有没有其他更好的方法呢?
了解排序算法的老哥可能已经猜到今天写什么啦。是滴,我们今天来写写用空间换时间的线性排序。
说之前我们先来回顾一下之前的排序算法,最好的时间复杂度为 O(nlogn) ,且都基于元素之间的比较来进行排序,
我们来说一下非基于元素比较的排序算法,且时间复杂度为 O(n),时间复杂度是线性的,所以我们称其为线性排序算法。
其优势在于在对一定范围内的整数排序时,它的复杂度为Ο(n+k),此时的 k 则代表整数的范围。快于任何一种比较类排序算法,不过也是需要牺牲一些空间来换取时间。
下面我们先来看看什么是计数排序,这个计数的含义是什么?
我们假设某一分店共有 10 名员工,
工龄分别为 1,2,3,5,0,2,2,4,5,9
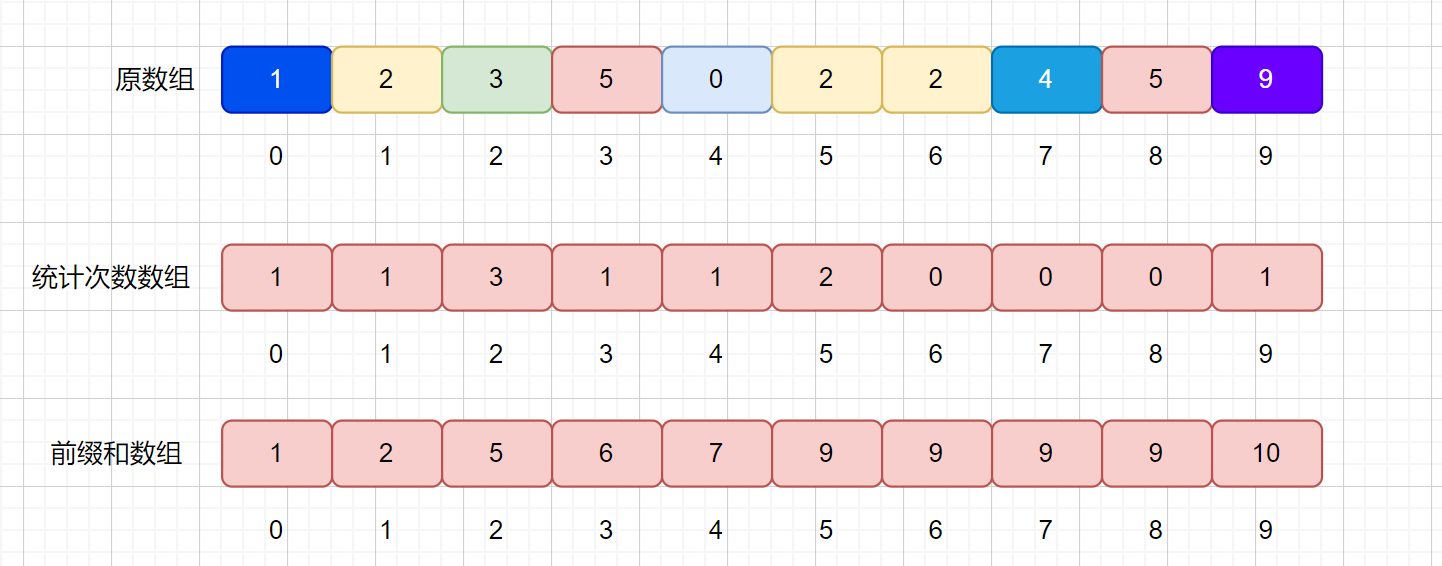
那么我们将其存在一个长度为 10 的数组里,,但是我们注意,我们数组此时存的并不是元素值,而是元素的个数。见下图
注:此时我们这里统计次数的数组根据最大值来决定,上面的例子中最大值为 9 ,则长度为 9 + 1 = 10。暂且先这样理解,后面会对其优化 。
我们继续以上图的例子来说明,在该数组中,索引代表的为元素值(也就是上面例子中的工龄),数组的值代表的则是元素个数(也就是不同工龄出现的次数)。
即工龄为 0 的员工有 1 个, 工龄为 1 的员工有 1 个,工龄为 2 的员工有 3 个 。。。
然后我们根据出现次数将其依次取出看看是什么效果。
0,1,2,2,2,3,4,5,5,9
我们发现此时元素则变成了有序的,但是这并不是排序,只是简单的按照统计数组的下标,输出了元素值,并没有真正的给原始数组进行排序。
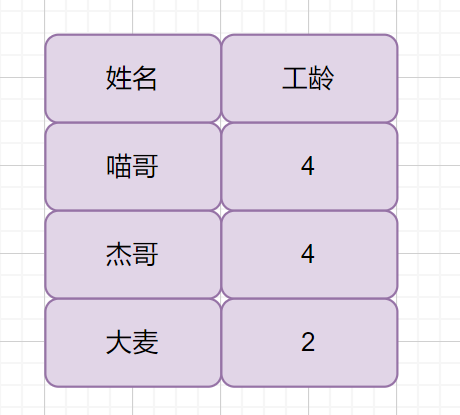
这样操作之后我们不知道工龄属于哪个员工。
见下图
虽然喵哥和杰哥工龄相同,如果我们按照上面的操作输出之后,我们不能知道工龄为 4 的两个员工,哪个是喵哥哪个是杰哥。
所以我们需要借助其他方法来对元素进行排序。
大家还记不记得我们之前说过的前缀和,下面我们通过上面统计次数的数组求出其前缀和数组。
因为我们是通过统计次数的数组得到了前缀和数组,那么我们来分析一下 presum 数组里面值的含义。
例如我们的 presum[2] = 5 ,代表的则是原数组小于等于 2 的值共有 5 个。presum[4] = 7 代表小于等于 4 的元素共有 7 个。
是不是感觉计数排序的含义要慢慢显现出来啦。
其实到这里我们已经可以理解的差不多了,还差最后一步,
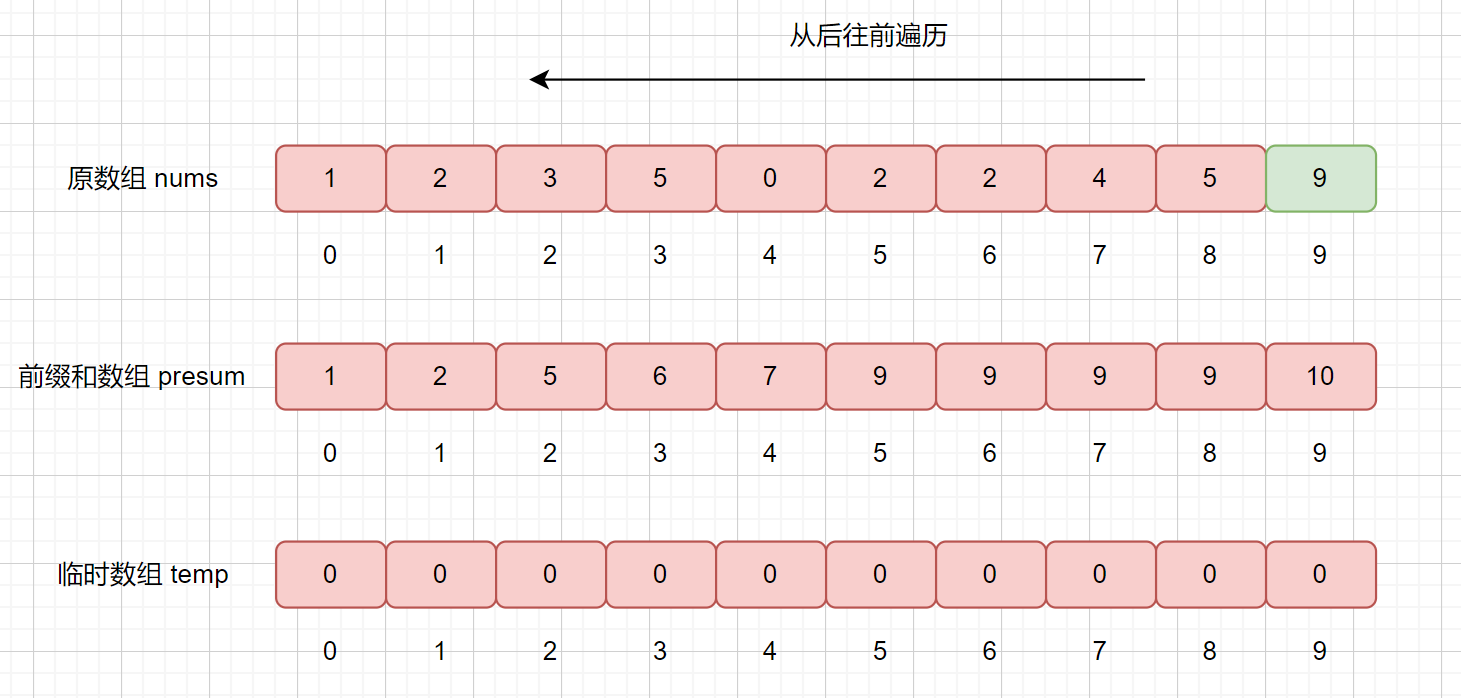
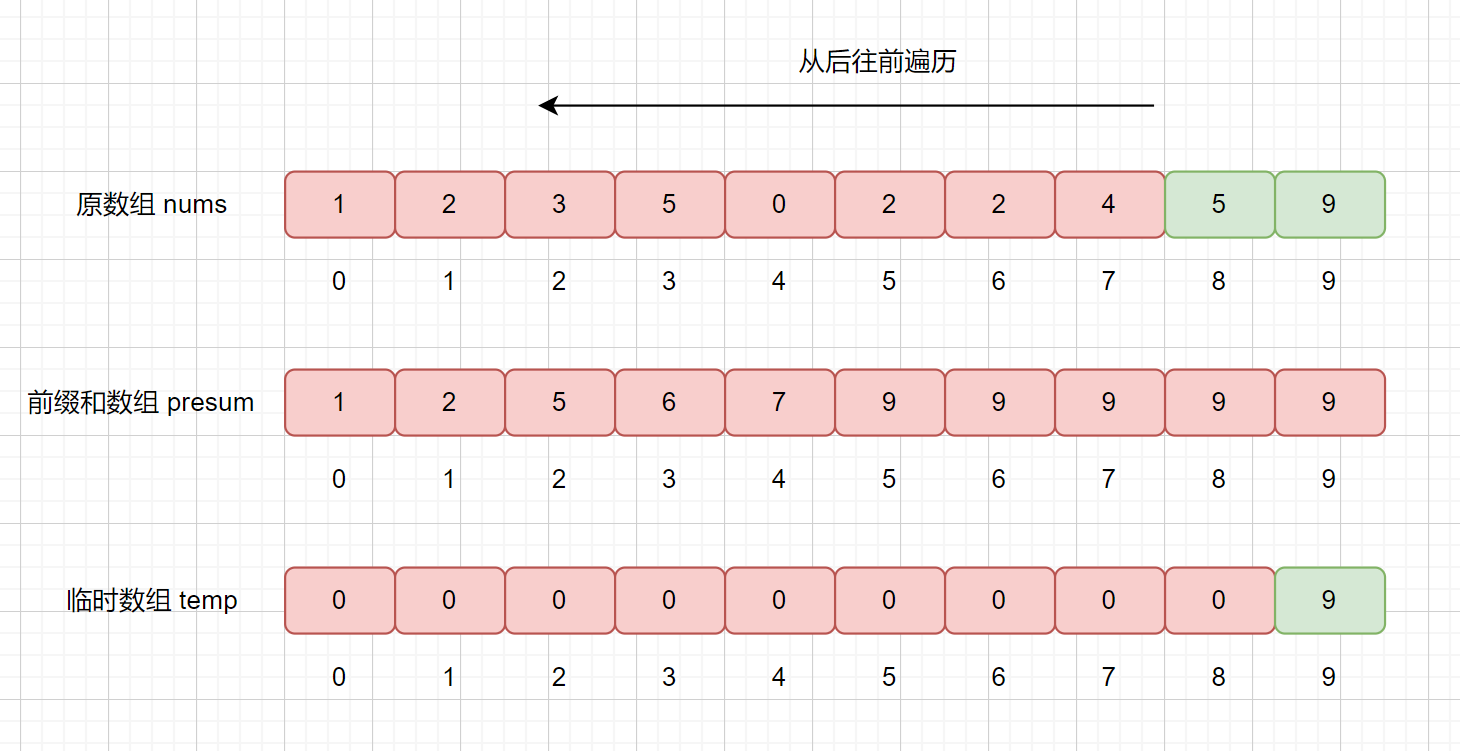
此时我们要从后往前遍历原始数组,然后将遍历到的元素放到临时数组的合适位置,并修改 presum 数组的值,遍历结束后则达到了排序的目的。
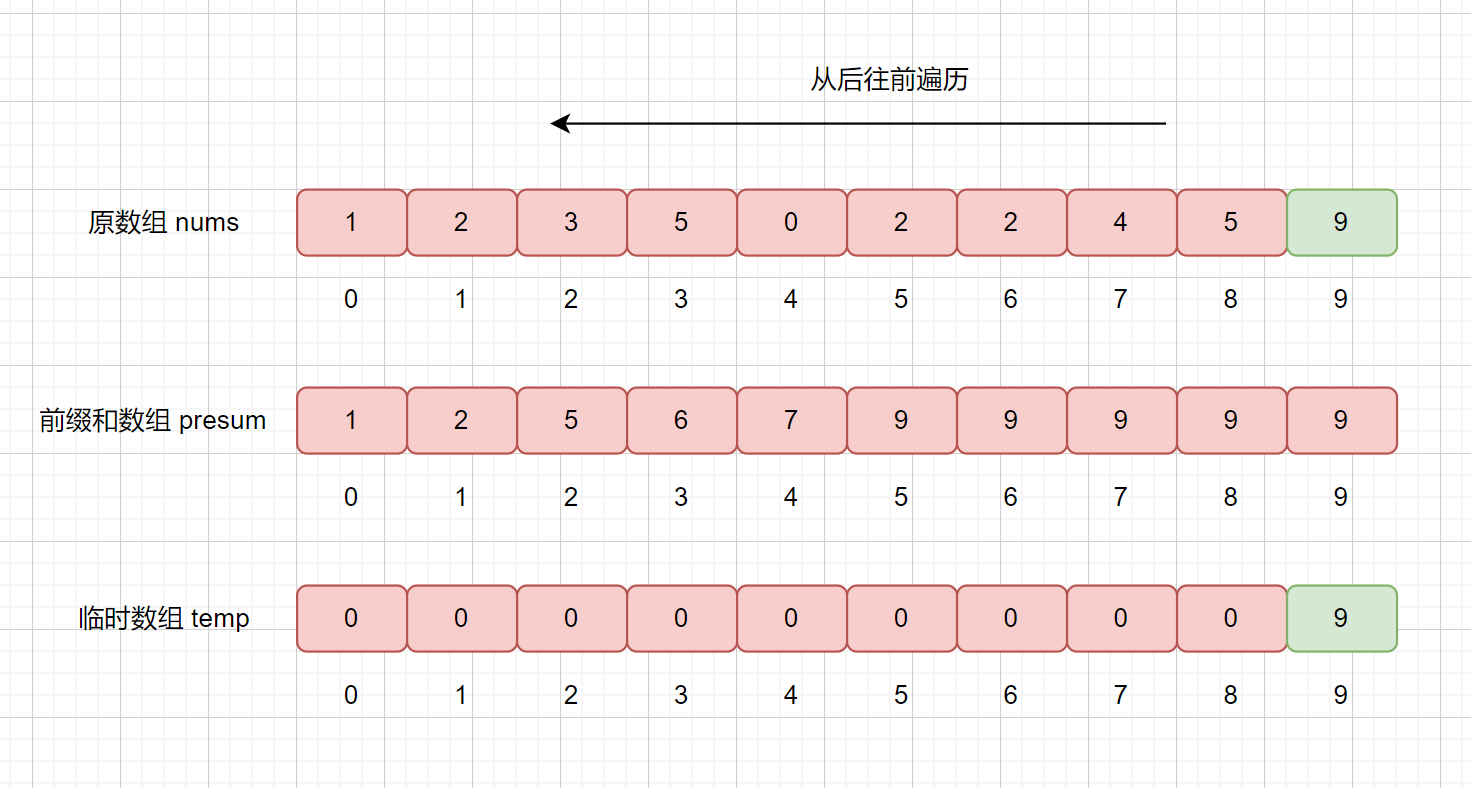
我们从后往前遍历,nums[9] = 9,则我们拿该值去 presum 数组中查找,发现 presum[nums[9]] = presum[9] = 10 ,大家还记得我们 presum 数组里面每个值得含义不,我们此时 presum[9] = 10,则代表在数组中,小于等于的数共有 10 个,则我们要将他排在临时数组的第 10 个位置,也就是 temp[9] = 9。
我们还需要干什么呢?我们想一下,我们已经把 9 放入到 temp 数组里了,已经对其排好序了,那么我们的 presum 数组则不应该再统计他了,则将相应的位置减 1 即可,也就是 presum[9] = 10 - 1 = 9;
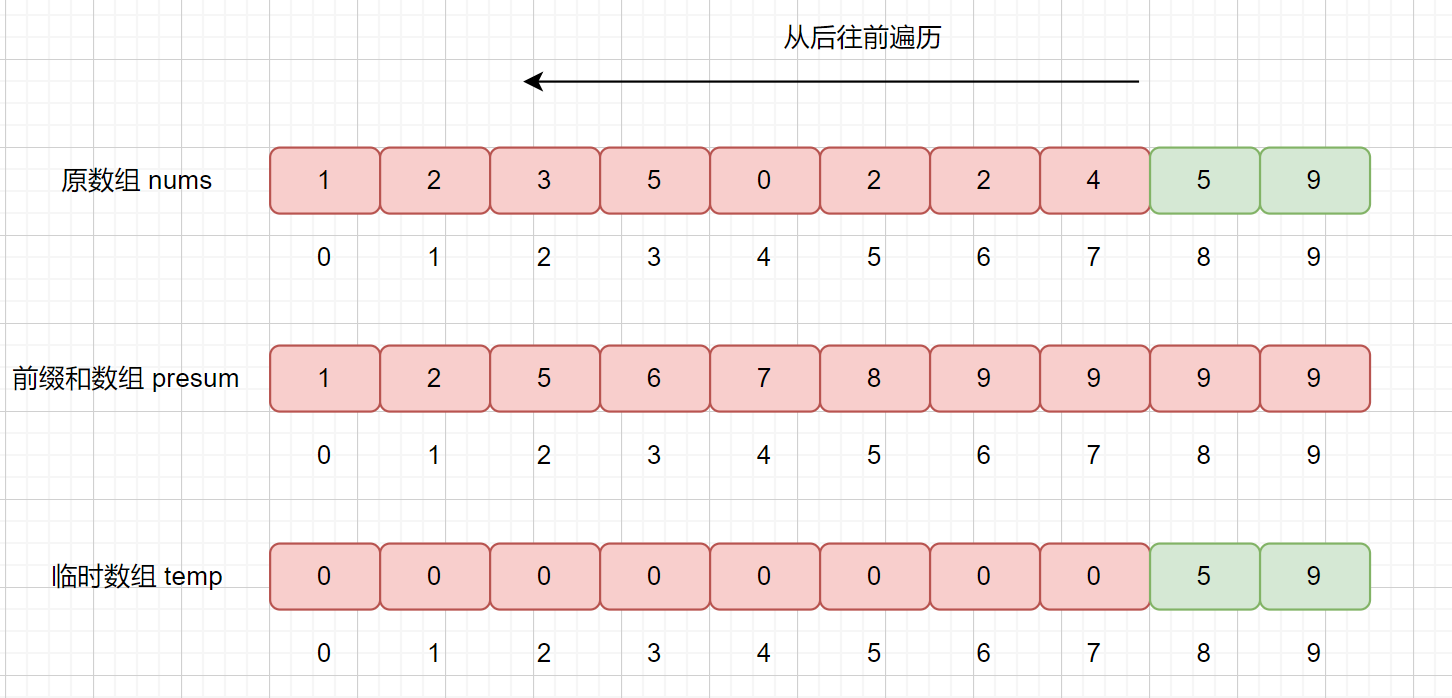
下面我们继续遍历 5 ,然后同样执行上诉步骤
我们继续查询 presum 数组,发现 presum[5] = 9,则说明小于等于 5 的数共有 9 个,我们将其放入到 temp 数组的第 9 个位置,也就是
temp[8] = 5。然后再将 presum[5] 减 1 。
是不是到这里就理解了计数排序的大致思路啦。
这个排序的过程像不像查字典呢?通过查询 presum 数组,得出自己应该排在临时数组的第几位。然后再修改下字典,直到遍历结束。
那么我们先来用动画模拟一下我们这个 bug 版的计数排序,加深理解。
注:我们得到 presum 数组的过程在动画中省略。直接模拟排序过程。
但是到现在就完了吗?显然没有,我们思考下这个情况。
假如我们的数字为 90,93,94,91,92 如果我们根据上面方法设置 presum 数组的长度,那我们则需要设置数组长度为 95(因为最大值是94),这样显然是不合理的,会浪费掉很多空间。
还有就是当我们需要对负数进行排序时同样会出现问题,因为我们求次数的时候是根据 nums[index] 的值来填充 presum 数组的,所以当 nums[index] 为负数时,填充 presum 数组时则会报错。而且此时通过最大值来定义数组长度也不合理。
所以我们需要采取别的方法来定义数组长度。
下面我们来说一下偏移量的概念。
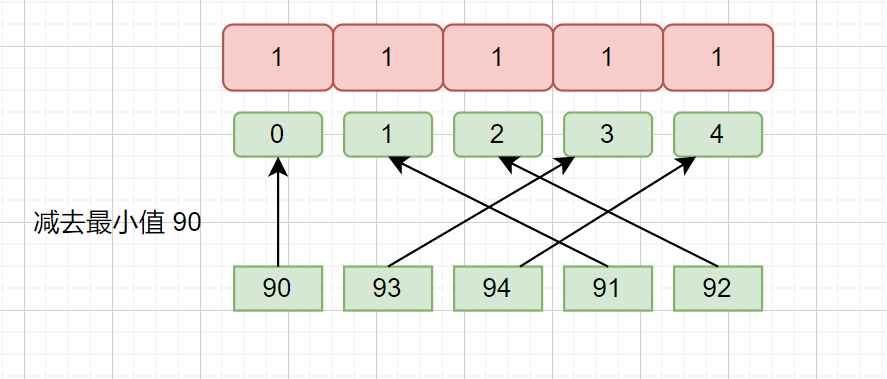
例如 90,93,94,91,92,我们 可以通过 max ,min 的值来设置数组长度即 94 - 90 + 1 = 5 。偏移量则为 min 值,也就是 90。
见下图。
这样我们填充 presum 数组时就不会出现浪费空间的情况了,负数?出现负数的情况当然也可以。继续看
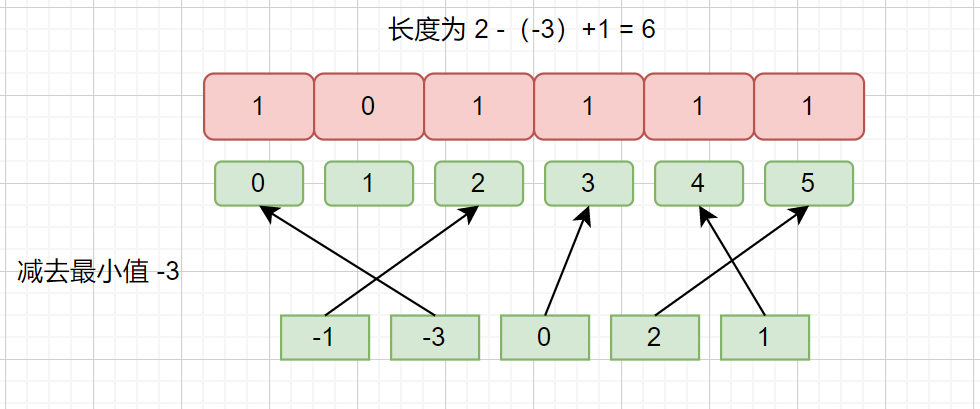
例如:-1,-3,0,2,1
一样可以,哦了,到这里我们就搞定了计数排序,下面我们来看一哈代码吧。
Java Code:
class Solution {
public int[] sortArray(int[] nums) {
int len = nums.length;
if (nums.length < 1) {
return nums;
}
//求出最大最小值
int max = nums[0];
int min = nums[0];
for (int x : nums) {
if (max < x) max = x;
if (min > x) min = x;
}
//设置 presum 数组长度,然后求出我们的前缀和数组,
//这里我们可以把求次数数组和前缀和数组用一个数组处理
int[] presum = new int[max-min+1];
for (int x : nums) {
presum[x-min]++;
}
for (int i = 1; i < presum.length; ++i) {
presum[i] = presum[i-1]+presum[i];
}
//临时数组
int[] temp = new int[len];
//遍历数组,开始排序,注意偏移量
for (int i = len-1; i >= 0; --i) {
//查找 presum 字典,然后将其放到临时数组,注意偏移度
int index = presum[nums[i]-min]-1;
temp[index] = nums[i];
//相应位置减一
presum[nums[i]-min]--;
}
//copy回原数组
System.arraycopy(temp,0,nums,0,len);
return nums;
}
}
Python Code:
from typing import List
class Solution:
def sortArray(self,nums: List[int])->List[int]:
leng = len(nums)
if leng < 1:
return nums
# 求出最大最小值
max = nums[0]
min = nums[0]
for x in nums:
if max < x:
max = x
if min > x:
min = x
# 设置 presum 数组长度,然后求出我们的前缀和数组,
# 这里我们可以把求次数数组和前缀和数组用一个数组处理
presum = [0] * (max - min + 1)
for x in nums:
presum[x - min] += 1
for i in range(1, len(presum)):
presum[i] = presum[i - 1] + presum[i]
# 临时数组
temp = [0] * leng
# 遍历数组,开始排序,注意偏移量
for i in range(leng - 1, -1, -1):
# 查找 presum 字典,然后将其放到临时数组,注意偏移度
index = presum[nums[i] - min] - 1
temp[index] = nums[i]
# 相应位置减一
presum[nums[i] - min] -= 1
# copy回原数组
nums = temp
return nums
好啦,这个排序算法我们已经搞定了,下面我们来扒一扒它。
计数排序时间复杂度分析
我们的总体运算量为 n+n+k+n ,总体运算是 3n + k 所以时间复杂度为 O(N+K);
计数排序空间复杂度分析
我们用到了辅助数组,空间复杂度为 O(n)
计数排序稳定性分析
稳定性在我们最后存入临时数组时有体现,我们当时让其放入临时数组的合适位置,并减一,所以某元素前面的相同元素,在临时数组,仍然在其前面。所以计数排序是稳定的排序算法。
虽然计数排序效率不错但是用到的并不多。
-
这是因为其当数组元素的范围太大时,并不适合计数排序,不仅浪费时间,效率还会大大降低。
-
当待排序的元素非整数时,也不适用,大家思考一下这是为什么呢?
好啦,今天的文章就到这啦,我们下期再见,拜了个拜.