5.5 KiB
KMP算法(Knuth-Morris-Pratt)
我们刚才讲了 BM 算法,虽然不是特别容易理解,但是如果你用心看的话肯定可以看懂的,我们再来看一个新的算法,这个算法是考研时必考的算法。实际上 BM 和 KMP 算法的本质是一样的,你理解了 BM 再来理解 KMP 那就是分分钟的事啦。
我们先来看一个实例
为了让读者更容易理解,我们将指针移动改成了模式串移动,两者相对与主串的移动是一致的,重新比较时都是从指针位置继续比较。
通过上面的实例是不是很快就能理解 KMP 算法的思想了,但是 KMP 的难点不是在这里,不过多思考,认真看理解起来也是很轻松的。
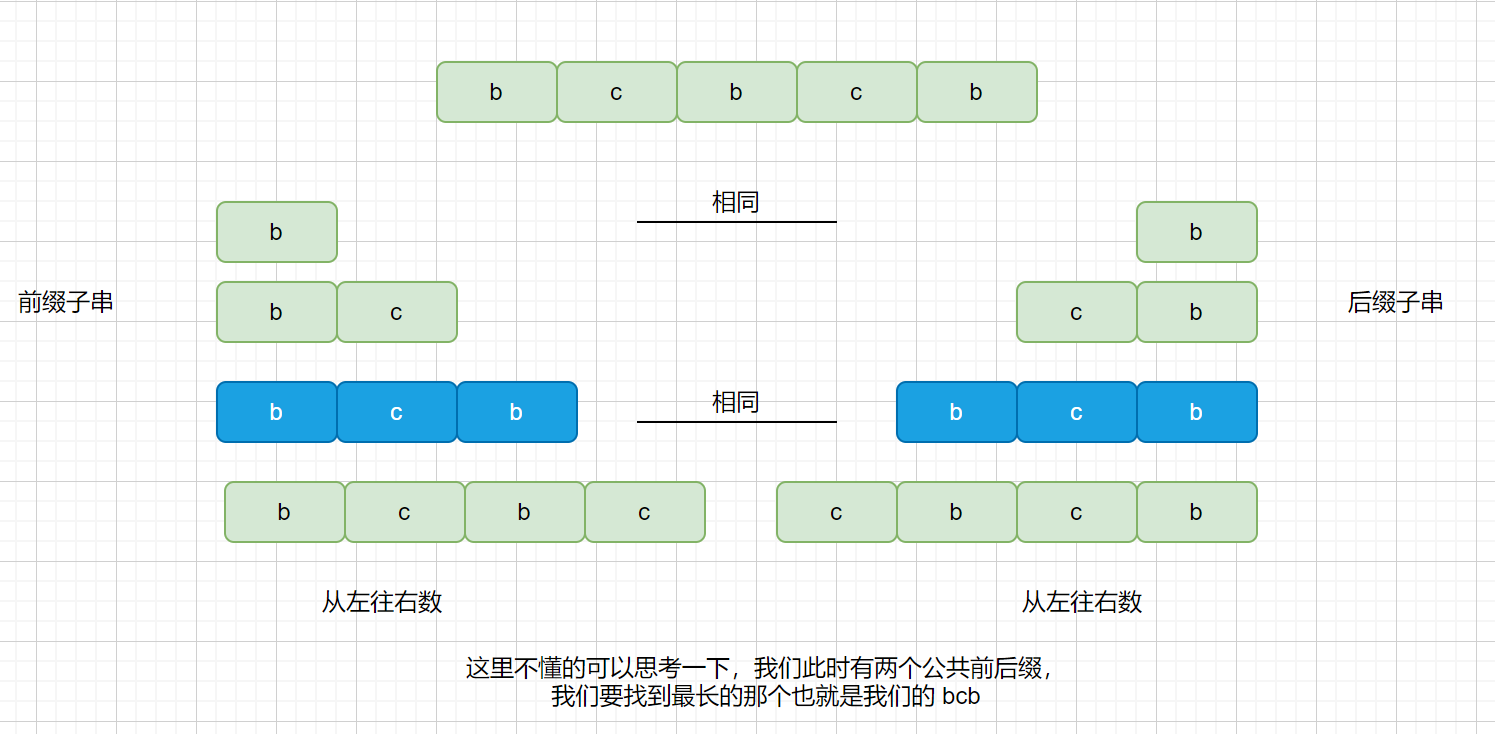
在上面的例子中我们提到了一个名词,最长公共前后缀,这个是什么意思呢?下面我们通过一个较简单的例子进行描述。
此时我们在红色阴影处匹配失败,绿色为匹配成功部分,则我们观察匹配成功的部分。
我们来看一下匹配成功部分的所有前缀
我们的最长公共前后缀如下图,则我们需要这样移动
好啦,看完上面的图,KMP的核心原理已经基本搞定了,但是我们现在的问题是,我们应该怎么才能知道他的最长公共前后缀的长度是多少呢?怎么知道移动多少位呢?
刚才我们在 BM 中说到,我们移动位数跟主串无关,只跟模式串有关,跟我们的 bc,suffix,prefix 数组的值有关,我们通过这些数组就可以知道我们每次移动多少位啦,其实 KMP 也有一个数组,这个数组叫做 next 数组,那么这个 next 数组存的是什么呢?
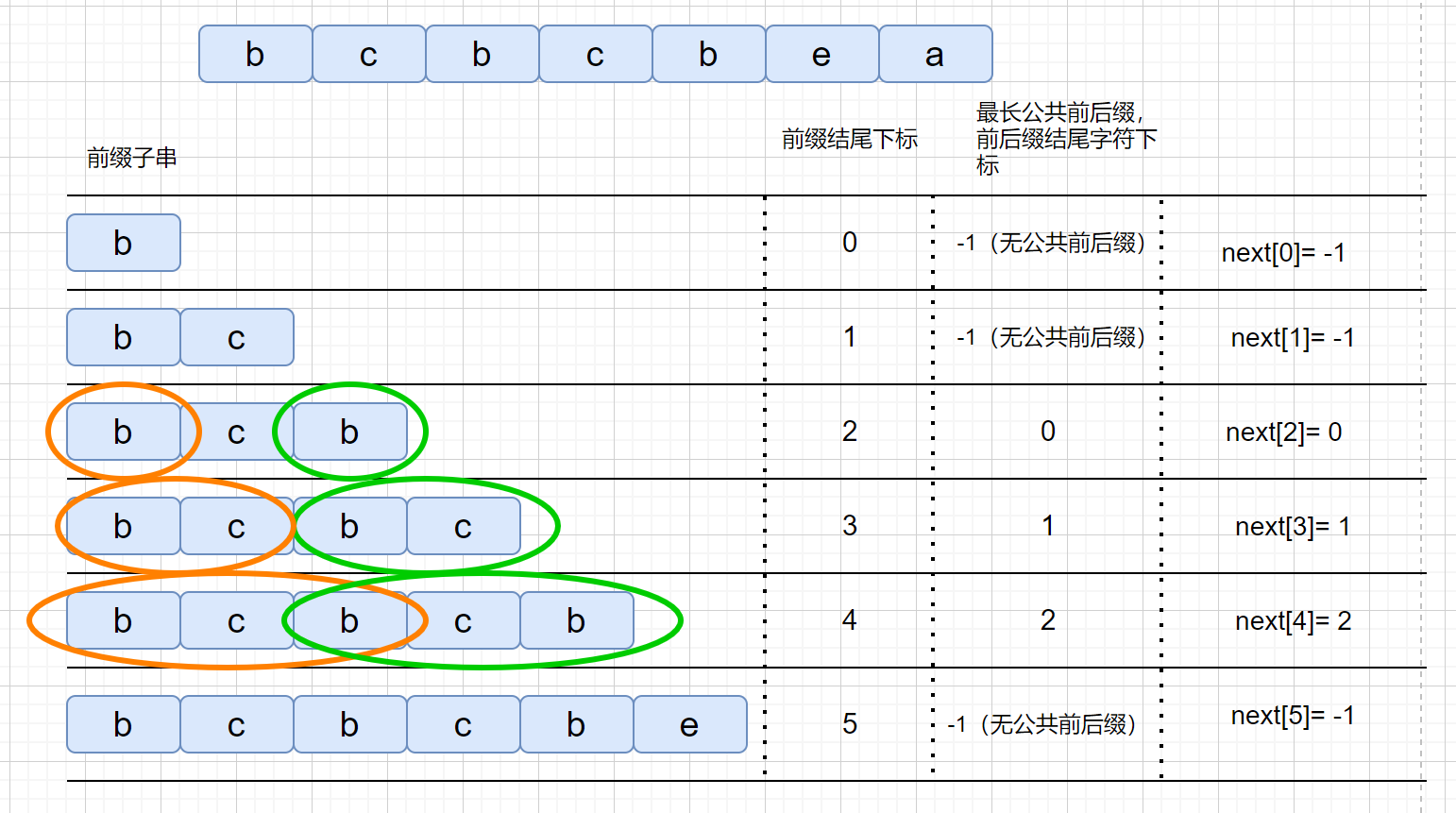
next 数组存的咱们最长公共前后缀中,前缀的结尾字符下标。是不是感觉有点别扭,我们通过一个例子进行说明。
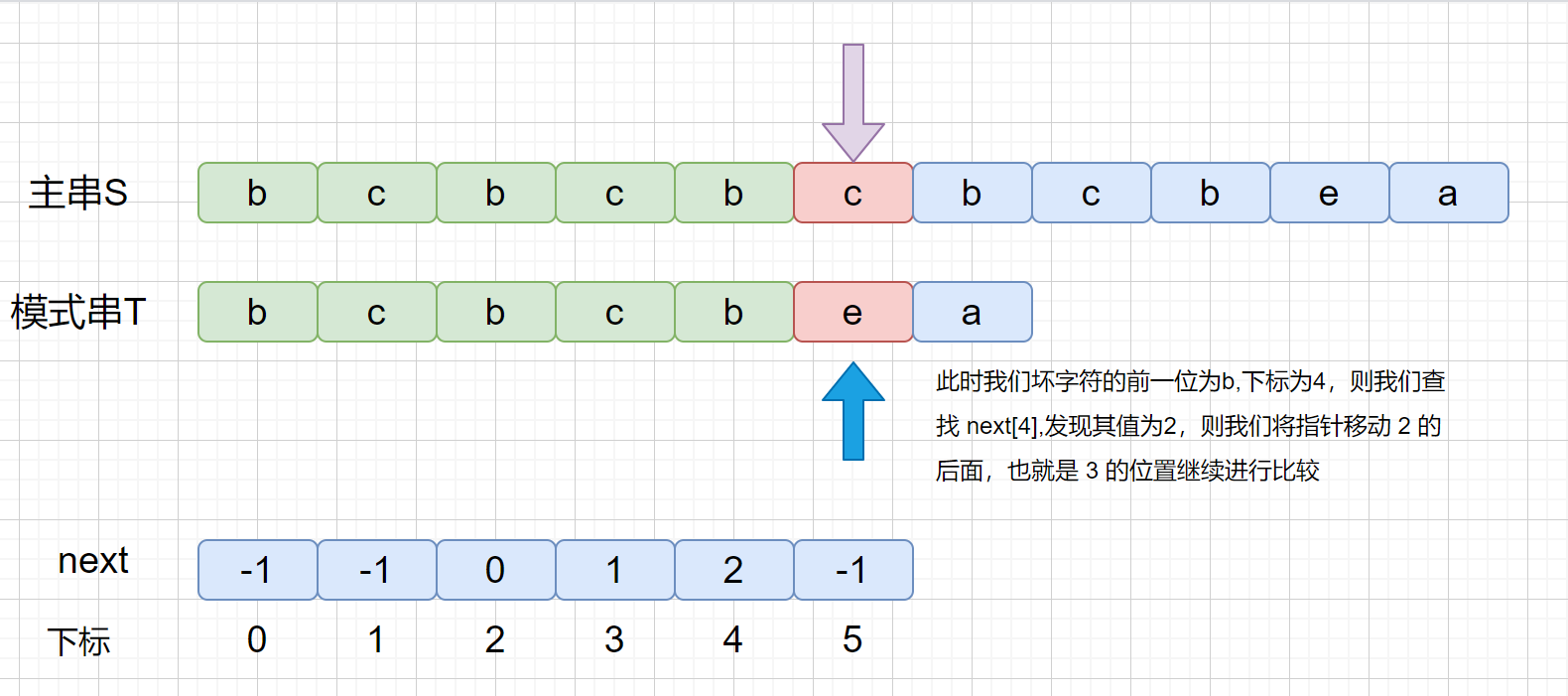
我们知道 next 数组之后,我们的 KMP 算法实现起来就很容易啦,另外我们看一下 next 数组到底是干什么用的。
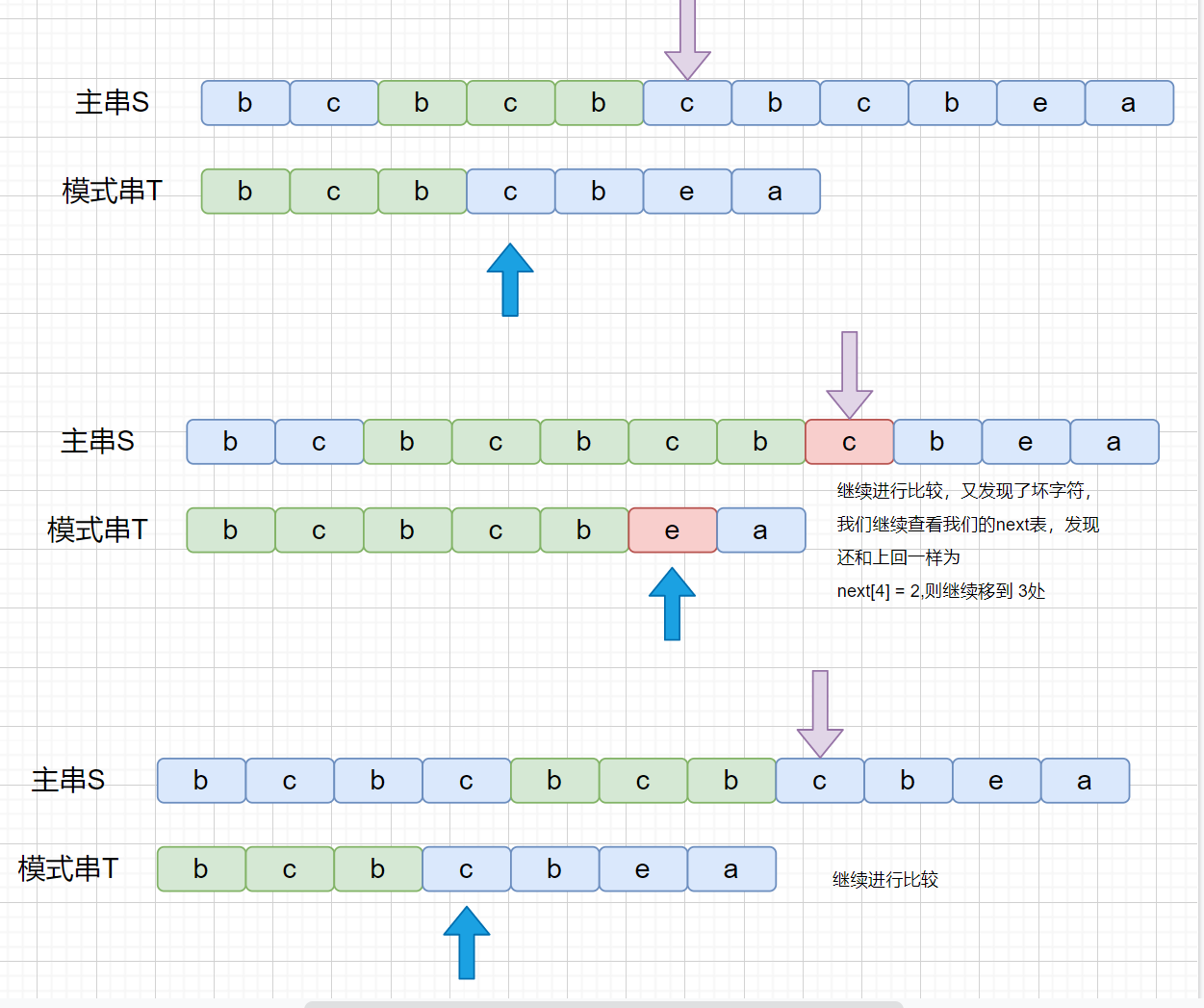
剩下的就不用说啦,完全一致啦,咱们将上面这个例子,翻译成和咱们开头对应的动画大家看一下。
下面我们看一下代码,标有详细注释,大家认真看呀。
注:很多教科书的 next 数组表示方式不一致,理解即可
class Solution {
public int strStr(String haystack, String needle) {
//两种特殊情况
if (needle.length() == 0) {
return 0;
}
if (haystack.length() == 0) {
return -1;
}
// char 数组
char[] hasyarr = haystack.toCharArray();
char[] nearr = needle.toCharArray();
//长度
int halen = hasyarr.length;
int nelen = nearr.length;
//返回下标
return kmp(hasyarr,halen,nearr,nelen);
}
public int kmp (char[] hasyarr, int halen, char[] nearr, int nelen) {
//获取next 数组
int[] next = next(nearr,nelen);
int j = 0;
for (int i = 0; i < halen; ++i) {
//发现不匹配的字符,然后根据 next 数组移动指针,移动到最大公共前后缀的,
//前缀的后一位,和咱们移动模式串的含义相同
while (j > 0 && hasyarr[i] != nearr[j]) {
j = next[j - 1] + 1;
//超出长度时,可以直接返回不存在
if (nelen - j + i > halen) {
return -1;
}
}
//如果相同就将指针同时后移一下,比较下个字符
if (hasyarr[i] == nearr[j]) {
++j;
}
//遍历完整个模式串,返回模式串的起点下标
if (j == nelen) {
return i - nelen + 1;
}
}
return -1;
}
//这一块比较难懂,不想看的同学可以忽略,了解大致含义即可,或者自己调试一下,看看运行情况
//我会每一步都写上注释
public int[] next (char[] needle,int len) {
//定义 next 数组
int[] next = new int[len];
// 初始化
next[0] = -1;
int k = -1;
for (int i = 1; i < len; ++i) {
//我们此时知道了 [0,i-1]的最长前后缀,但是k+1的指向的值和i不相同时,我们则需要回溯
//因为 next[k]就时用来记录子串的最长公共前后缀的尾坐标(即长度)
//就要找 k+1前一个元素在next数组里的值,即next[k+1]
while (k != -1 && needle[k + 1] != needle[i]) {
k = next[k];
}
// 相同情况,就是 k的下一位,和 i 相同时,此时我们已经知道 [0,i-1]的最长前后缀
//然后 k - 1 又和 i 相同,最长前后缀加1,即可
if (needle[k+1] == needle[i]) {
++k;
}
next[i] = k;
}
return next;
}
}