krahets 33d79ea6da Update docs for deployment on Vercel.

2022-11-22 17:47:26 +08:00

22 KiB

Raw Blame History

comments
true

时间复杂度

统计算法运行时间

运行时间能够直观且准确地体现出算法的效率水平。如果我们想要 准确预估一段代码的运行时间 ，该如何做呢？

首先需要 确定运行平台 ，包括硬件配置、编程语言、系统环境等，这些都会影响到代码的运行效率。
评估 各种计算操作的所需运行时间 ，例如加法操作 + 需要 1 ns ，乘法操作 * 需要 10 ns ，打印操作需要 5 ns 等。
根据代码 统计所有计算操作的数量 ，并将所有操作的执行时间求和，即可得到运行时间。

例如以下代码，输入数据大小为 n ，根据以上方法，可以得到算法运行时间为 6n + 12 ns 。


1 + 1 + 10 + (1 + 5) \times n  = 6n + 12

=== "Java"

```java title=""
// 在某运行平台下
void algorithm(int n) {
    int a = 2;  // 1 ns
    a = a + 1;  // 1 ns
    a = a * 2;  // 10 ns
    // 循环 n 次
    for (int i = 0; i < n; i++) {  // 1 ns ，每轮都要执行 i++
        System.out.println(0);     // 5 ns
    }
}
```

=== "C++"

```cpp title=""

```

=== "Python"

```python title=""

```

但实际上， 统计算法的运行时间既不合理也不现实。 首先，我们不希望预估时间和运行平台绑定，毕竟算法需要跑在各式各样的平台之上。其次，我们很难获知每一种操作的运行时间，这为预估过程带来了极大的难度。

统计时间增长趋势

「时间复杂度分析」采取了不同的做法，其统计的不是算法运行时间，而是 算法运行时间随着数据量变大时的增长趋势 。

“时间增长趋势” 这个概念比较抽象，我们借助一个例子来理解。设输入数据大小为 n ，给定三个算法 A , B , C 。

算法 A 只有 1 个打印操作，算法运行时间不随着 n 增大而增长。我们称此算法的时间复杂度为「常数阶」。
算法 B 中的打印操作需要循环 n 次，算法运行时间随着 n 增大成线性增长。此算法的时间复杂度被称为「线性阶」。
算法 C 中的打印操作需要循环 1000000 次，但运行时间仍与输入数据大小 n 无关。因此 C 的时间复杂度和 A 相同，仍为「常数阶」。

=== "Java"

```java title=""
// 算法 A 时间复杂度：常数阶
void algorithm_A(int n) {
    System.out.println(0);
}
// 算法 B 时间复杂度：线性阶
void algorithm_B(int n) {
    for (int i = 0; i < n; i++) {
        System.out.println(0);
    }
}
// 算法 C 时间复杂度：常数阶
void algorithm_C(int n) {
    for (int i = 0; i < 1000000; i++) {
        System.out.println(0);
    }
}
```

=== "C++"

```cpp title=""

```

=== "Python"

```python title=""

```

Fig. 算法 A, B, C 的时间增长趋势

相比直接统计算法运行时间，时间复杂度分析的做法有什么好处呢？以及有什么不足？

时间复杂度可以有效评估算法效率。 算法 B 运行时间的增长是线性的，在 n > 1 时慢于算法 A ，在 n > 1000000 时慢于算法 C 。实质上，只要输入数据大小 n 足够大，复杂度为「常数阶」的算法一定优于「线性阶」的算法，这也正是时间增长趋势的含义。

时间复杂度分析将统计「计算操作的运行时间」简化为统计「计算操作的数量」。 这是因为，无论是运行平台、还是计算操作类型，都与算法运行时间的增长趋势无关。因此，我们可以简单地将所有计算操作的执行时间统一看作是相同的 “单位时间” 。

时间复杂度也存在一定的局限性。 比如，虽然算法 A 和 C 的时间复杂度相同，但是实际的运行时间有非常大的差别。再比如，虽然算法 B 比 C 的时间复杂度要更高，但在输入数据大小 n 比较小时，算法 B 是要明显优于算法 C 的。即使存在这些问题，计算复杂度仍然是评判算法效率的最有效、最常用方法。

函数渐进上界

设算法「计算操作数量」为 T(n) ，其是一个关于输入数据大小 n 的函数。例如，以下算法的操作数量为


T(n) = 3 + 2n

=== "Java"

```java title=""
void algorithm(int n) {
    int a = 1;  // +1
    a = a + 1;  // +1
    a = a * 2;  // +1
    // 循环 n 次
    for (int i = 0; i < n; i++) { // +1（每轮都执行 i ++）
        System.out.println(0);    // +1
    }
}
```

=== "C++"

```cpp title=""

```

=== "Python"

```python title=""

```

T(n) 是个一次函数，说明时间增长趋势是线性的，因此易得时间复杂度是线性阶。

我们将线性阶的时间复杂度记为 O(n) ，这个数学符号被称为「大 O 记号 Big-O Notation」，代表函数 T(n) 的「渐进上界 asymptotic upper bound」。

我们要推算时间复杂度，本质上是在计算「操作数量函数 T(n) 」的渐进上界。下面我们先来看看函数渐进上界的数学定义。

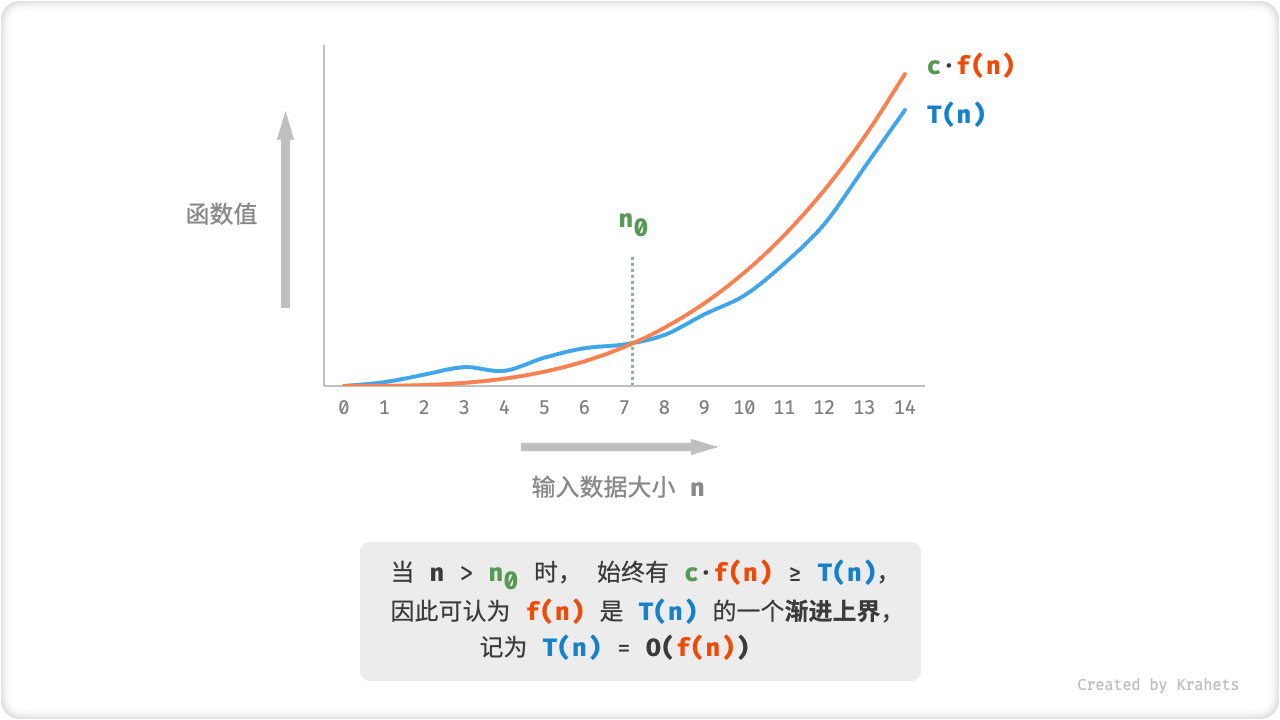
!!! abstract "函数渐进上界"

若存在正实数 $c$ 和实数 $n_0$ ，使得对于所有的 $n > n_0$ ，均有
$$
T(n) \leq c \cdot f(n)
$$
则可认为 $f(n)$ 给出了 $T(n)$ 的一个渐进上界，记为 
$$
T(n) = O(f(n))
$$

Fig. 函数的渐进上界

本质上看，计算渐进上界就是在找一个函数 f(n) ，使得在 n 趋向于无穷大时，T(n) 和 f(n) 处于相同的增长级别（仅相差一个常数项 c 的倍数）。

!!! tip

渐进上界的数学味儿有点重，如果你感觉没有完全理解，无需担心，因为在实际使用中我们只需要会推算即可，数学意义可以慢慢领悟。

推算方法

推算出 f(n) 后，我们就得到时间复杂度 O(f(n)) 。那么，如何来确定渐进上界 f(n) 呢？总体分为两步，首先「统计操作数量」，然后「判断渐进上界」。

1. 统计操作数量

对着代码，从上到下一行一行地计数即可。然而，由于上述 c \cdot f(n) 中的常数项 c 可以取任意大小，因此操作数量 T(n) 中的各种系数、常数项都可以被忽略。根据此原则，可以总结出以下计数偷懒技巧：

跳过数量与 n 无关的操作。 因为他们都是 T(n) 中的常数项，对时间复杂度不产生影响。
省略所有系数。 例如，循环 2n 次、5n + 1 次、……，都可以化简记为 n 次，因为 n 前面的系数对时间复杂度也不产生影响。
循环嵌套时使用乘法。 总操作数量等于外层循环和内层循环操作数量之积，每一层循环依然可以分别套用上述 1. 和 2. 技巧。

根据以下示例，使用上述技巧前、后的统计结果分别为


\begin{aligned}
T(n) & = 2n(n + 1) + (5n + 1) + 2 & \text{完整统计 (-.-|||)} \newline
& = 2n^2 + 7n + 3 \newline
T(n) & = n^2 + n & \text{偷懒统计 (o.O)}
\end{aligned}

最终，两者都能推出相同的时间复杂度结果，即 O(n^2) 。

=== "Java"

```java title=""
void algorithm(int n) {
    int a = 1;  // +0（技巧 1）
    a = a + n;  // +0（技巧 1）
    // +n（技巧 2）
    for (int i = 0; i < 5 * n + 1; i++) {
        System.out.println(0);
    }
    // +n*n（技巧 3）
    for (int i = 0; i < 2 * n; i++) {
        for (int j = 0; j < n + 1; j++) {
            System.out.println(0);
        }
    }
}
```

=== "C++"

```cpp title=""

```

=== "Python"

```python title=""

```

2. 判断渐进上界

时间复杂度由多项式 T(n) 中最高阶的项来决定。这是因为在 n 趋于无穷大时，最高阶的项将处于主导作用，其它项的影响都可以被忽略。

以下表格给出了一些例子，其中有一些夸张的值，是想要向大家强调 系数无法撼动阶数 这一结论。在 n 趋于无穷大时，这些常数都是 “浮云” 。

操作数量 `T(n)`	时间复杂度 `O(f(n))`
`100000`	`O(1)`
`3n + 2`	`O(n)`
`2n^2 + 3n + 2`	`O(n^2)`
`n^3 + 10000n^2`	`O(n^3)`
`2^n + 10000n^{10000}`	`O(2^n)`

常见类型

设输入数据大小为 n ，常见的时间复杂度类型有（从低到高排列）


\begin{aligned}
O(1) < O(\log n) < O(n) < O(n \log n) < O(n^2) < O(2^n) < O(n!) \newline
\text{常数阶} < \text{对数阶} < \text{线性阶} < \text{线性对数阶} < \text{平方阶} < \text{指数阶} < \text{阶乘阶}
\end{aligned}

Fig. 时间复杂度的常见类型

!!! tip

部分示例代码需要一些前置知识，包括数组、递归算法等。如果遇到看不懂的地方无需担心，可以在学习完后面章节后再来复习，现阶段先聚焦在理解时间复杂度含义和推算方法上。

常数阶 `O(1)`

常数阶的操作数量与输入数据大小 n 无关，即不随着 n 的变化而变化。

对于以下算法，无论操作数量 size 有多大，只要与数据大小 n 无关，时间复杂度就仍为 O(1) 。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 常数阶 */
int constant(int n) {
    int count = 0;
    int size = 100000;
    for (int i = 0; i < size; i++)
        count++;
    return count;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

线性阶 `O(n)`

线性阶的操作数量相对输入数据大小成线性级别增长。线性阶常出现于单层循环。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 线性阶 */
int linear(int n) {
    int count = 0;
    for (int i = 0; i < n; i++)
        count++;
    return count;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

「遍历数组」和「遍历链表」等操作，时间复杂度都为 O(n) ，其中 n 为数组或链表的长度。

!!! tip

**数据大小 $n$ 是根据输入数据的类型来确定的。** 比如，在上述示例中，我们直接将 $n$ 看作输入数据大小；以下遍历数组示例中，数据大小 $n$ 为数组的长度。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 线性阶（遍历数组） */
int arrayTraversal(int[] nums) {
    int count = 0;
    // 循环次数与数组长度成正比
    for (int num : nums) {
        count++;
    }
    return count;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

平方阶 `O(n^2)`

平方阶的操作数量相对输入数据大小成平方级别增长。平方阶常出现于嵌套循环，外层循环和内层循环都为 O(n) ，总体为 O(n^2) 。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 平方阶 */
int quadratic(int n) {
    int count = 0;
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++) {
            count++;
        }
    }
    return count;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

Fig. 常数阶、线性阶、平方阶的时间复杂度

以「冒泡排序」为例，外层循环 n - 1 次，内层循环 n-1, n-2, \cdots, 2, 1 次，平均为 \frac{n}{2} 次，因此时间复杂度为 O(n^2) 。


O((n - 1) \frac{n}{2}) = O(n^2)

=== "Java"

```java title="" title="time_complexity_types.java"
/* 平方阶（冒泡排序） */
void bubbleSort(int[] nums) {
    int n = nums.length;
    for (int i = 0; i < n - 1; i++) {
        for (int j = 0; j < n - 1 - i; j++) {
            if (nums[j] > nums[j + 1]) {
                // 交换 nums[j] 和 nums[j + 1]
                int tmp = nums[j];
                nums[j] = nums[j + 1];
                nums[j + 1] = tmp;
            }
        }
    }
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

指数阶 `O(2^n)`

!!! note

生物学科中的 “细胞分裂” 即是指数阶增长：初始状态为 $1$ 个细胞，分裂一轮后为 $2$ 个，分裂两轮后为 $4$ 个，……，分裂 $n$ 轮后有 $2^n$ 个细胞。

指数阶增长地非常快，在实际应用中一般是不能被接受的。若一个问题使用「暴力枚举」求解的时间复杂度是 O(2^n) ，那么一般都需要使用「动态规划」或「贪心算法」等算法来求解。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 指数阶（遍历实现） */
int exponential(int n) {
    int count = 0, base = 1;
    // cell 每轮一分为二，形成数列 1, 2, 4, 8, ..., 2^(n-1)
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < base; j++) {
            count++;
        }
        base *= 2;
    }
    // count = 1 + 2 + 4 + 8 + .. + 2^(n-1) = 2^n - 1
    return count;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

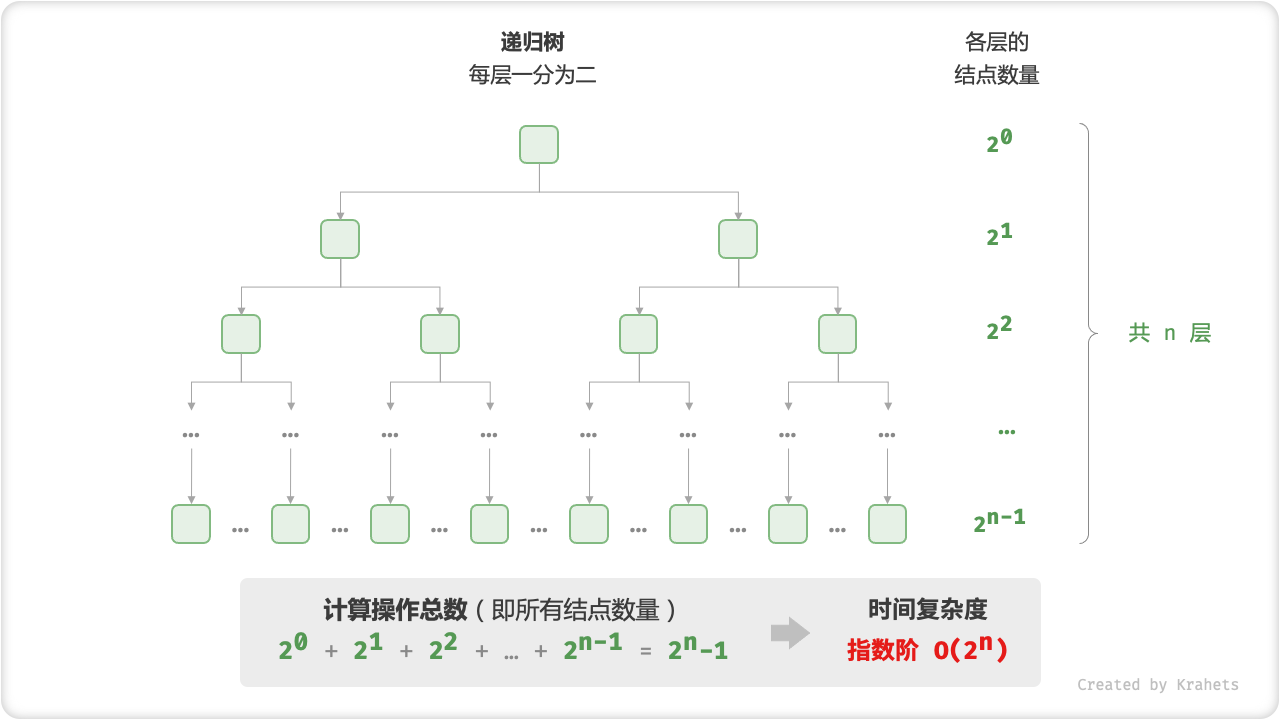
Fig. 指数阶的时间复杂度

在实际算法中，指数阶常出现于递归函数。例如以下代码，不断地一分为二，分裂 n 次后停止。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 指数阶（递归实现） */
int expRecur(int n) {
    if (n == 1) return 1;
    return expRecur(n - 1) + expRecur(n - 1) + 1;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

对数阶 `O(\log n)`

对数阶与指数阶正好相反，后者反映 “每轮增加到两倍的情况” ，而前者反映 “每轮缩减到一半的情况” 。对数阶仅次于常数阶，时间增长的很慢，是理想的时间复杂度。

对数阶常出现于「二分查找」和「分治算法」中，体现 “一分为多” 、“化繁为简” 的算法思想。

设输入数据大小为 n ，由于每轮缩减到一半，因此循环次数是 \log_2 n ，即 2^n 的反函数。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 对数阶（循环实现） */
int logarithmic(float n) {
    int count = 0;
    while (n > 1) {
        n = n / 2;
        count++;
    }
    return count;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

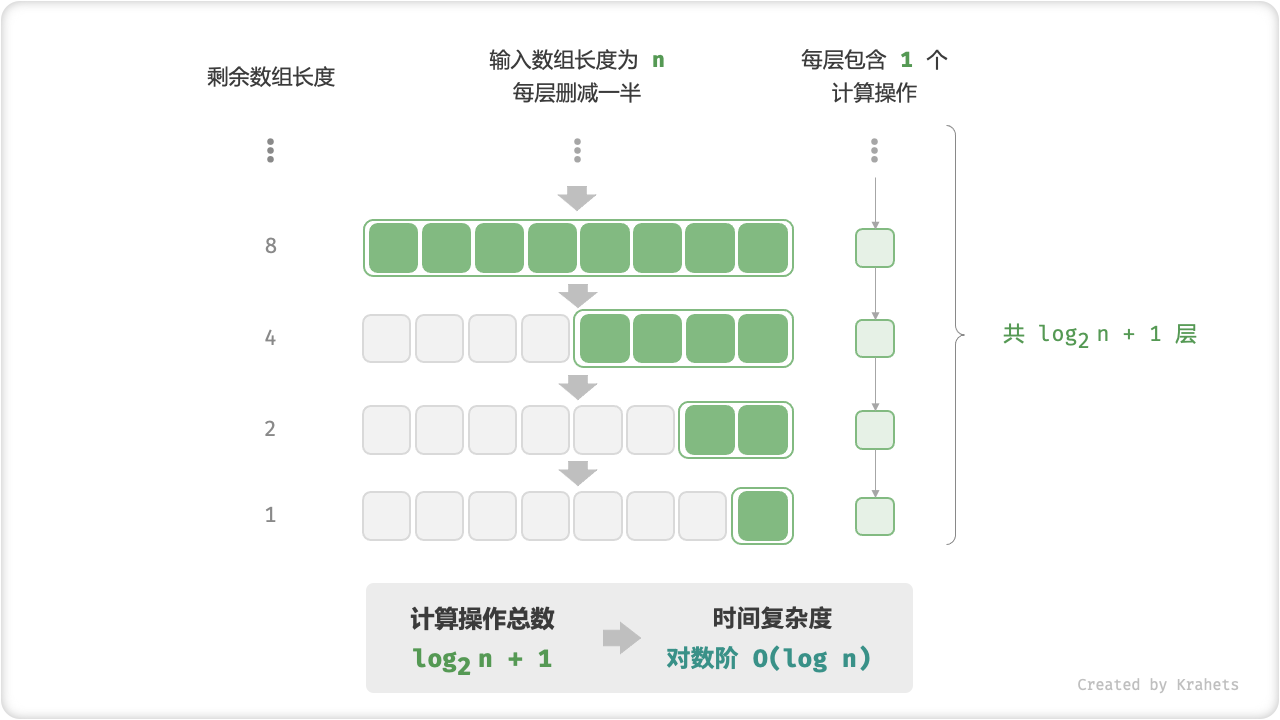
Fig. 对数阶的时间复杂度

与指数阶类似，对数阶也常出现于递归函数。以下代码形成了一个高度为 \log_2 n 的递归树。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 对数阶（递归实现） */
int logRecur(float n) {
    if (n <= 1) return 0;
    return logRecur(n / 2) + 1;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

线性对数阶 `O(n \log n)`

线性对数阶常出现于嵌套循环中，两层循环的时间复杂度分别为 O(\log n) 和 O(n) 。

主流排序算法的时间复杂度都是 O(n \log n ) ，例如快速排序、归并排序、堆排序等。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 线性对数阶 */
int linearLogRecur(float n) {
    if (n <= 1) return 1;
    int count = linearLogRecur(n / 2) + 
                linearLogRecur(n / 2);
    for (int i = 0; i < n; i++) {
        count++;
    }
    return count;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

Fig. 线性对数阶的时间复杂度

阶乘阶 `O(n!)`

阶乘阶对应数学上的「全排列」。即给定 n 个互不重复的元素，求其所有可能的排列方案，则方案数量为


n! = n \times (n - 1) \times (n - 2) \times \cdots \times 2 \times 1

阶乘常使用递归实现。例如以下代码，第一层分裂出 n 个，第二层分裂出 n - 1 个，…… ，直至到第 n 层时终止分裂。

=== "Java"

```java title="" title="time_complexity_types.java"
/* 阶乘阶（递归实现） */
int factorialRecur(int n) {
    if (n == 0) return 1;
    int count = 0;
    // 从 1 个分裂出 n 个
    for (int i = 0; i < n; i++) {
        count += factorialRecur(n - 1);
    }
    return count;
}
```

=== "C++"

```cpp title="time_complexity_types.cpp"

```

=== "Python"

```python title="time_complexity_types.py"

```

Fig. 阶乘阶的时间复杂度

最差、最佳、平均时间复杂度

某些算法的时间复杂度不是恒定的，而是与输入数据的分布有关。 举一个例子，输入一个长度为 n 数组 nums ，其中 nums 由从 1 至 n 的数字组成，但元素顺序是随机打乱的；算法的任务是返回元素 1 的索引。我们可以得出以下结论：

当 nums = [?, ?, ..., 1]，即当末尾元素是 1 时，则需完整遍历数组，此时达到 最差时间复杂度 $O(n)$ ；
当 nums = [1, ?, ?, ...] ，即当首个数字为 1 时，无论数组多长都不需要继续遍历，此时达到 最佳时间复杂度 $\Omega(1)$ ；

「函数渐进上界」使用大 O 记号表示，代表「最差时间复杂度」。与之对应，「函数渐进下界」用 \Omega 记号（Omega Notation）来表示，代表「最佳时间复杂度」。

=== "Java"

```java title="" title="worst_best_time_complexity.java"
public class worst_best_time_complexity {
    /* 生成一个数组，元素为 { 1, 2, ..., n }，顺序被打乱 */
    static int[] randomNumbers(int n) {
        Integer[] nums = new Integer[n];
        // 生成数组 nums = { 1, 2, 3, ..., n }
        for (int i = 0; i < n; i++) {
            nums[i] = i + 1;
        }
        // 随机打乱数组元素
        Collections.shuffle(Arrays.asList(nums));
        // Integer[] -> int[]
        int[] res = new int[n];
        for (int i = 0; i < n; i++) {
            res[i] = nums[i];
        }
        return res;
    }

    /* 查找数组 nums 中数字 1 所在索引 */
    static int findOne(int[] nums) {
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] == 1)
                return i;
        }
        return -1;
    }
    
    /* Driver Code */
    public static void main(String[] args) {
        for (int i = 0; i < 10; i++) {
            int n = 100;
            int[] nums = randomNumbers(n);
            int index = findOne(nums);
            System.out.println("打乱后的数组为 " + Arrays.toString(nums));
            System.out.println("数字 1 的索引为 " + index);
        }
    }
}
```

=== "C++"

```cpp title="worst_best_time_complexity.cpp"

```

=== "Python"

```python title="worst_best_time_complexity.py"

```

!!! tip

我们在实际应用中很少使用「最佳时间复杂度」，因为往往只有很小概率下才能达到，会带来一定的误导性。反之，「最差时间复杂度」最为实用，因为它给出了一个 “效率安全值” ，让我们可以放心地使用算法。

从上述示例可以看出，最差或最佳时间复杂度只出现在 “特殊分布的数据” 中，这些情况的出现概率往往很小，因此并不能最真实地反映算法运行效率。相对地，「平均时间复杂度」可以体现算法在随机输入数据下的运行效率，用 \Theta 记号（Theta Notation）来表示。

对于部分算法，我们可以简单地推算出随机数据分布下的平均情况。比如上述示例，由于输入数组是被打乱的，因此元素 1 出现在任意索引的概率都是相等的，那么算法的平均循环次数则是数组长度的一半 \frac{n}{2} ，平均时间复杂度为 \Theta(\frac{n}{2}) = \Theta(n) 。

但在实际应用中，尤其是较为复杂的算法，计算平均时间复杂度比较困难，因为很难简便地分析出在数据分布下的整体数学期望。这种情况下，我们一般使用最差时间复杂度来作为算法效率的评判标准。

22 KiB Raw Blame History Unescape Escape

时间复杂度

统计算法运行时间

统计时间增长趋势

函数渐进上界

推算方法

1. 统计操作数量

2. 判断渐进上界

常见类型

常数阶 O(1)

线性阶 O(n)

平方阶 O(n^2)

指数阶 O(2^n)

对数阶 O(\log n)

线性对数阶 O(n \log n)

阶乘阶 O(n!)

最差、最佳、平均时间复杂度

22 KiB

Raw Blame History

常数阶 `O(1)`

线性阶 `O(n)`

平方阶 `O(n^2)`

指数阶 `O(2^n)`

对数阶 `O(\log n)`

线性对数阶 `O(n \log n)`

阶乘阶 `O(n!)`