mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2025-10-13 11:52:59 +00:00
二叉树
This commit is contained in:
@@ -87,9 +87,11 @@
|
||||
- [【动画模拟】堆排序](https://github.com/chefyuan/algorithm-base/blob/main/animation-simulation/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E5%92%8C%E7%AE%97%E6%B3%95/%E5%A0%86%E6%8E%92%E5%BA%8F.md)
|
||||
- [【动画模拟】计数排序](https://github.com/chefyuan/algorithm-base/blob/main/animation-simulation/%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E5%92%8C%E7%AE%97%E6%B3%95/%E8%AE%A1%E6%95%B0%E6%8E%92%E5%BA%8F.md)
|
||||
|
||||
### 🍺二叉树基础
|
||||
### 🍺二叉树
|
||||
|
||||
- [前序遍历(迭代+Morris)](https://github.com/chefyuan/algorithm-base/blob/main/animation-simulation/%E4%BA%8C%E5%8F%89%E6%A0%91/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E5%89%8D%E5%BA%8F%E9%81%8D%E5%8E%86(%E6%A0%88).md)
|
||||
- [【动画模拟】前序遍历(迭代+Morris)](https://github.com/chefyuan/algorithm-base/blob/main/animation-simulation/%E4%BA%8C%E5%8F%89%E6%A0%91/%E4%BA%8C%E5%8F%89%E6%A0%91%E7%9A%84%E5%89%8D%E5%BA%8F%E9%81%8D%E5%8E%86(%E6%A0%88).md)
|
||||
- 【动画模拟】中序遍历(迭代+Morris)
|
||||
- 【动画模拟】后序遍历(迭代+Morris)
|
||||
|
||||
### 🍗排序算法秒杀题目
|
||||
|
||||
@@ -265,4 +267,4 @@
|
||||
|
||||
<div align="center"> <img src="https://cdn.jsdelivr.net/gh/tan45du/photobed@master/赞赏码.2mrhxsmxexa0.png" width = "200px" hight = "200px"/> </div>
|
||||
|
||||
####
|
||||
###### ####
|
||||
157
animation-simulation/二叉树/二叉树中序遍历.md
Normal file
157
animation-simulation/二叉树/二叉树中序遍历.md
Normal file
@@ -0,0 +1,157 @@
|
||||
哈喽大家好,我是厨子,之前我们说了二叉树前序遍历的迭代法和 Morris,今天咱们写一下中序遍历的迭代法和 Morris。
|
||||
|
||||
> 注:数据结构掌握不熟练的同学,阅读该文章之前,可以先阅读这两篇文章,二叉树基础,前序遍历另外喜欢电脑阅读的同学,可以在小屋后台回复仓库地址,获取 Github 链接进行阅读。
|
||||
|
||||
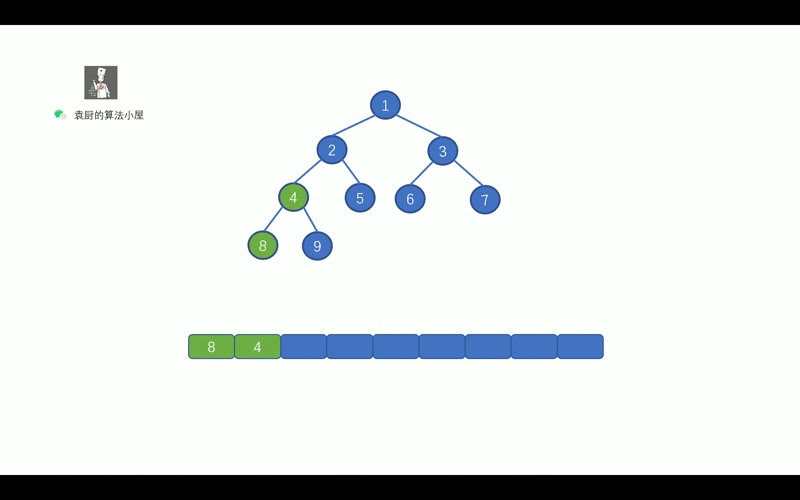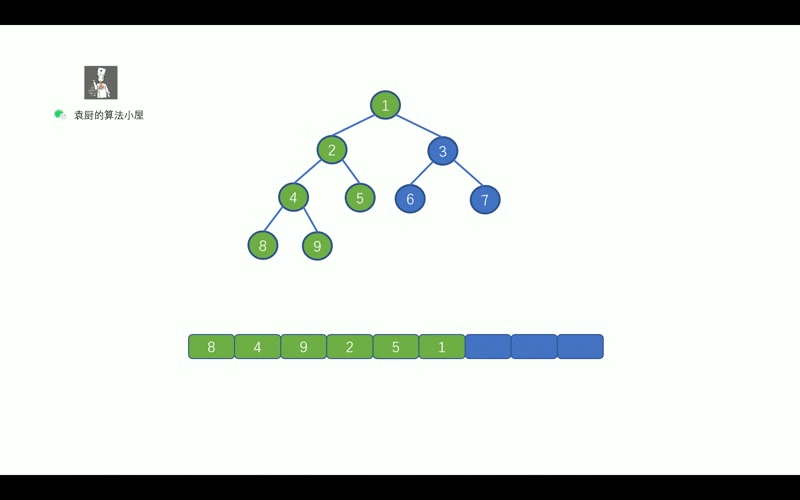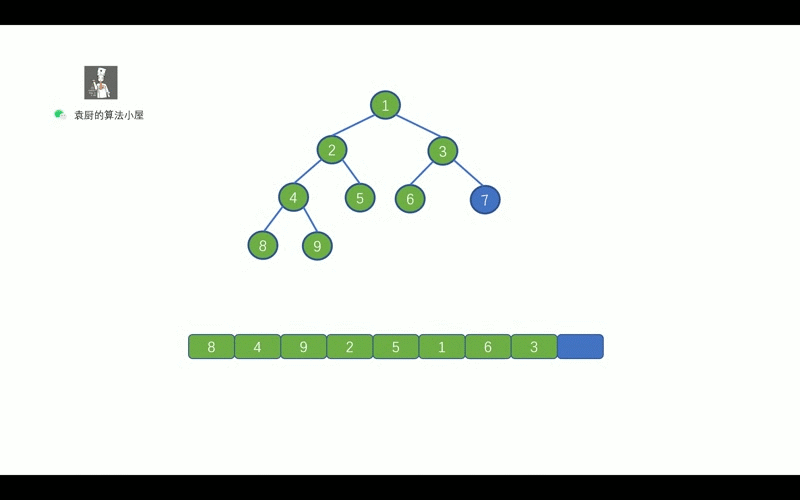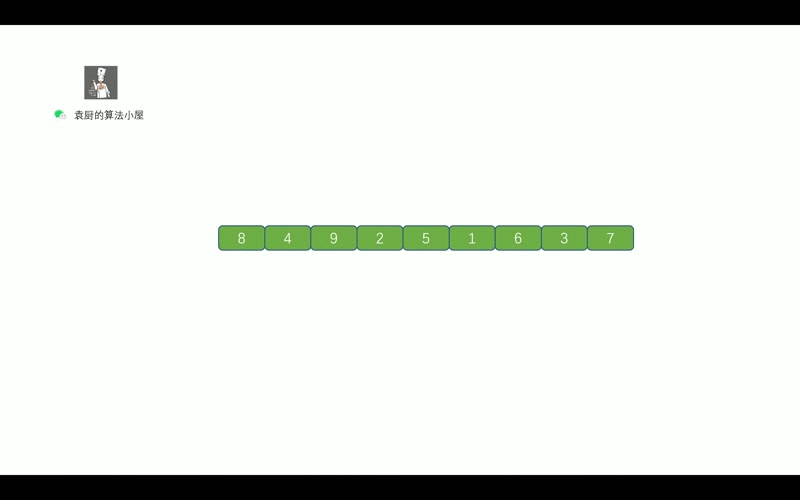
中序遍历的顺序是, `对于树中的某节点,先遍历该节点的左子树, 然后再遍历该节点, 最后遍历其右子树`。老规矩,上动画,我们先通过动画回忆一下二叉树的中序遍历。
|
||||
|
||||
|
||||
|
||||
注:二叉树基础总结大家可以阅读这篇文章,点我。
|
||||
|
||||
## 迭代法
|
||||
|
||||
我们二叉树的中序遍历迭代法和前序遍历是一样的,都是借助栈来帮助我们完成。
|
||||
|
||||
我们结合动画思考一下,该如何借助栈来实现呢?
|
||||
|
||||
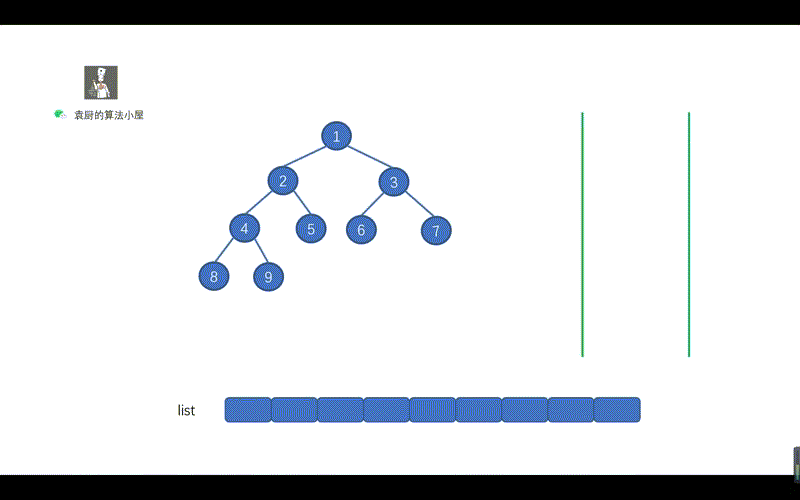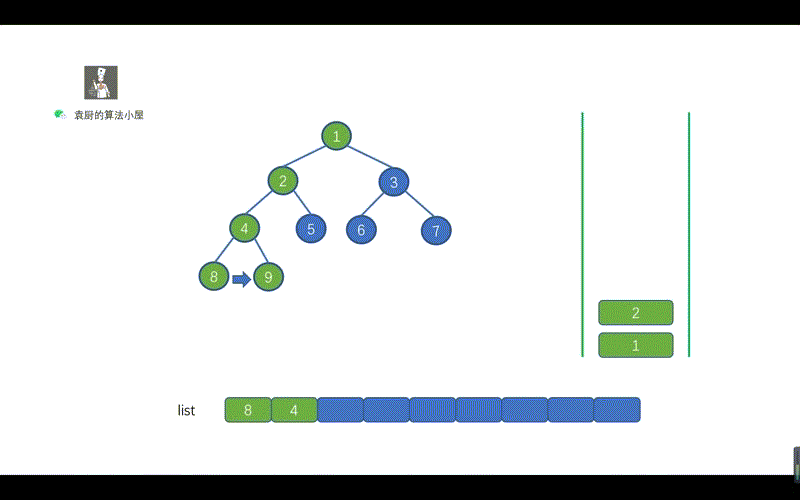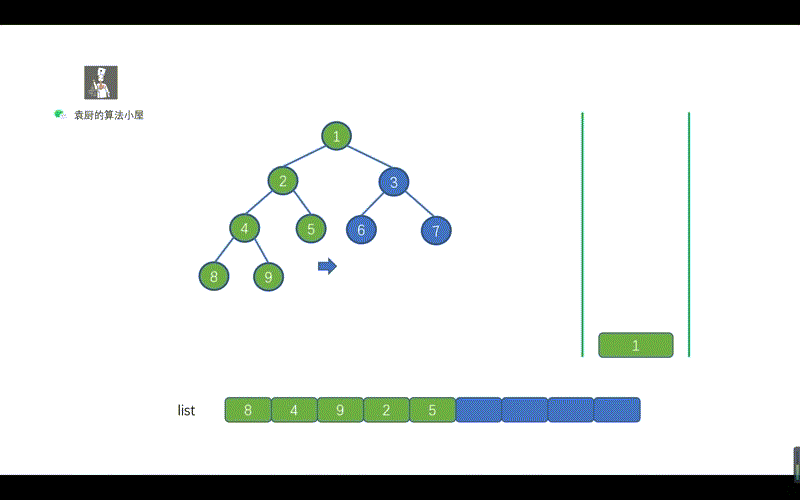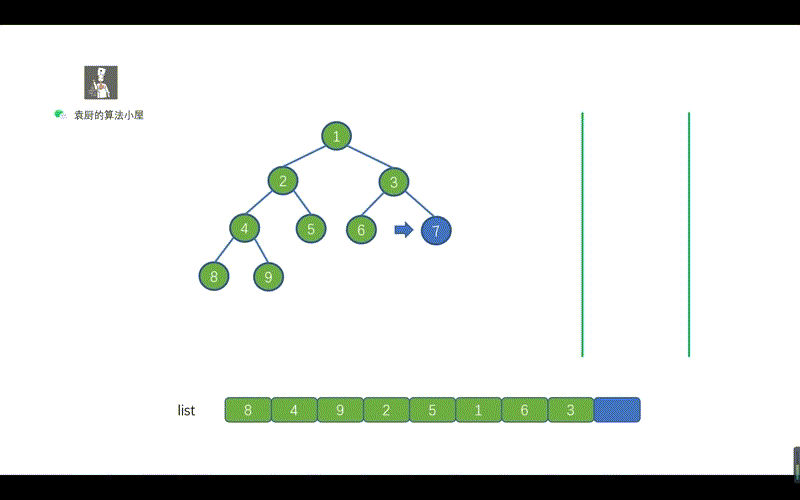
我们来看下面这个动画。
|
||||
|
||||
|
||||
|
||||
用栈实现的二叉树的中序遍历有两个关键的地方。
|
||||
|
||||
- 指针不断向节点的左孩子移动,为了找到我们当前需要遍历的节点。途中不断执行入栈操作
|
||||
- 当指针为空时,则开始出栈,并将指针指向出栈节点的右孩子。
|
||||
|
||||
这两个关键点也很容易理解,指针不断向左孩子移动,是为了找到我们此时需要节点。然后当指针指向空时,则说明我们此时已经找到该节点,执行出栈操作,并将其值存入 list 即可,另外我们需要将指针指向出栈节点的右孩子,迭代执行上诉操作。
|
||||
|
||||
大家是不是已经知道怎么写啦,下面我们看代码吧。
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public List<Integer> inorderTraversal(TreeNode root) {
|
||||
List<Integer> arr = new ArrayList<>();
|
||||
TreeNode cur = new TreeNode(-1);
|
||||
cur = root;
|
||||
Stack<TreeNode> stack = new Stack<>();
|
||||
while (!stack.isEmpty() || cur != null) {
|
||||
//找到当前应该遍历的那个节点
|
||||
while (cur != null) {
|
||||
stack.push(cur);
|
||||
cur = cur.left;
|
||||
}
|
||||
//此时指针指向空,也就是没有左子节点,则开始执行出栈操作
|
||||
TreeNode temp = stack.pop();
|
||||
arr.add(temp.val);
|
||||
//指向右子节点
|
||||
cur = temp.right;
|
||||
}
|
||||
return arr;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### **Morris**
|
||||
|
||||
我们之前说过,前序遍历的 Morris 方法,如果已经掌握,今天中序遍历的 Morris 方法也就没有什么难度,仅仅修改了一丢丢。
|
||||
|
||||
我们先来回顾一下前序遍历 Morris 方法的代码部分。
|
||||
|
||||
**前序遍历 Morris 代码**
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public List<Integer> preorderTraversal(TreeNode root) {
|
||||
|
||||
List<Integer> list = new ArrayList<>();
|
||||
if (root == null) {
|
||||
return list;
|
||||
}
|
||||
TreeNode p1 = root; TreeNode p2 = null;
|
||||
while (p1 != null) {
|
||||
p2 = p1.left;
|
||||
if (p2 != null) {
|
||||
//找到左子树的最右叶子节点
|
||||
while (p2.right != null && p2.right != p1) {
|
||||
p2 = p2.right;
|
||||
}
|
||||
//添加 right 指针,对应 right 指针为 null 的情况
|
||||
//标注 1
|
||||
if (p2.right == null) {
|
||||
list.add(p1.val);
|
||||
p2.right = p1;
|
||||
p1 = p1.left;
|
||||
continue;
|
||||
}
|
||||
//对应 right 指针存在的情况,则去掉 right 指针
|
||||
p2.right = null;
|
||||
//标注2
|
||||
} else {
|
||||
list.add(p1.val);
|
||||
}
|
||||
//移动 p1
|
||||
p1 = p1.right;
|
||||
}
|
||||
return list;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
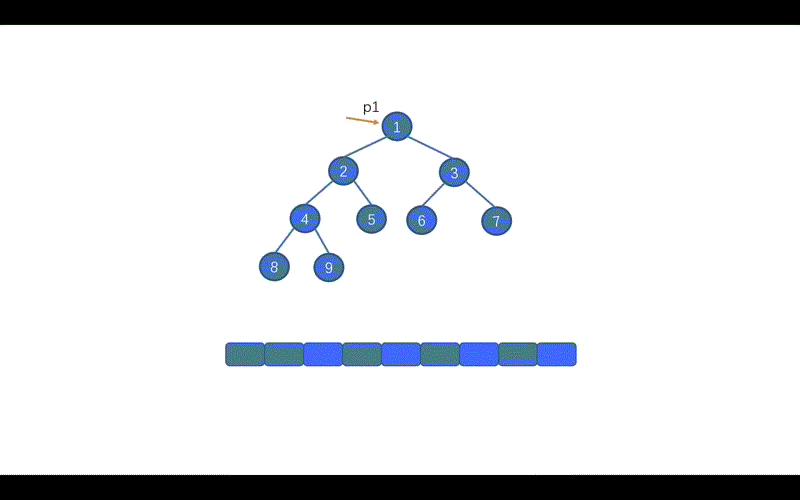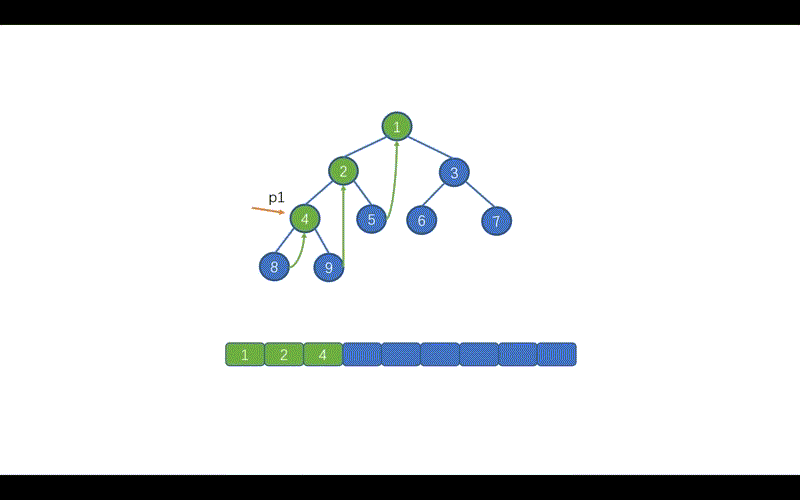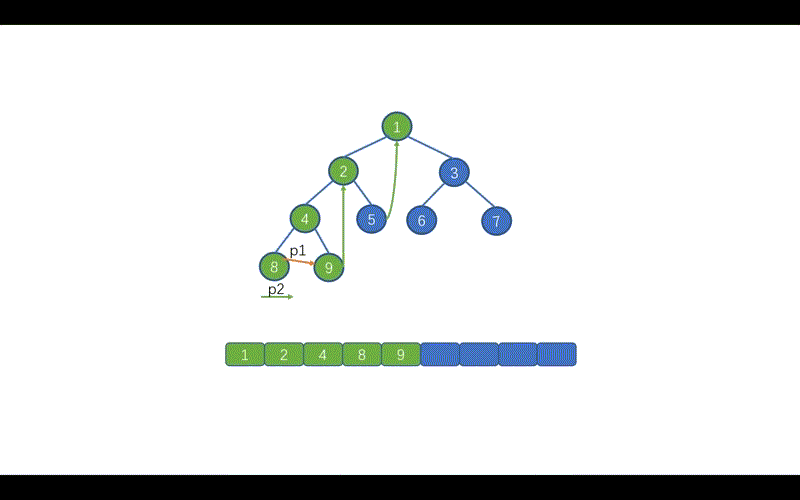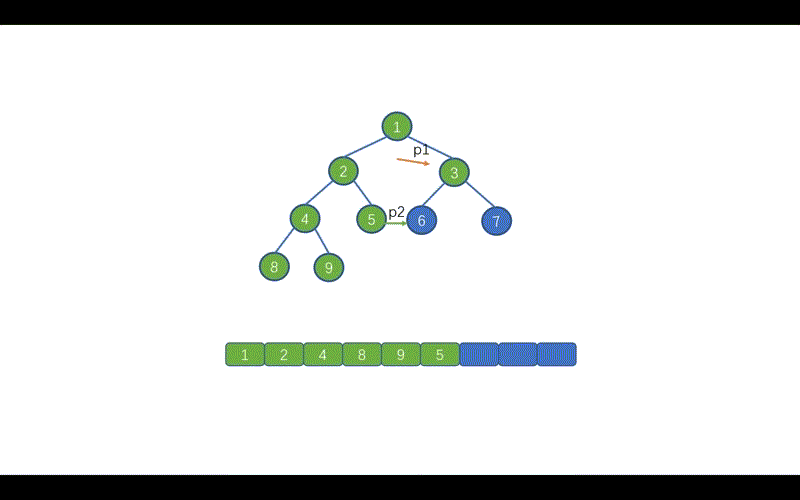
我们先来看标注 1 的部分,这里的含义是,当找到 p1 指向节点的左子树中的最右子节点时。也就是下图中的情况,此时我们需要将 p1 指向的节点值,存入 list。
|
||||
|
||||
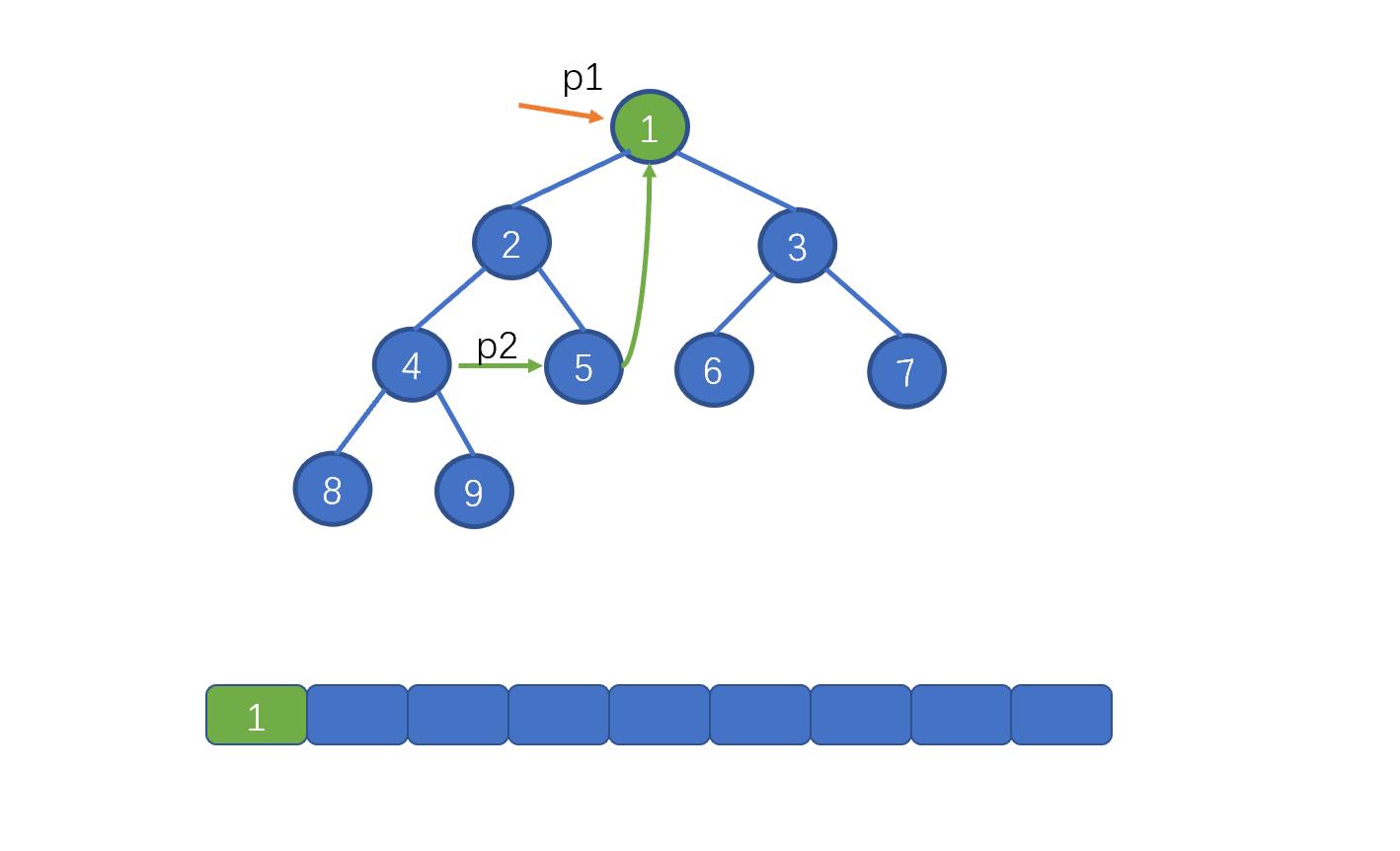
|
||||
|
||||
上述为前序遍历时的情况,那么中序遍历应该如何操作嘞。
|
||||
|
||||
前序遍历我们需要移动 p1 指针,`p1 = p1.left` 这样做的原因和上述迭代法原理一致,找到我们当前需要遍历的那个节点。
|
||||
|
||||
我们还需要修改哪里呢?见下图
|
||||
|
||||
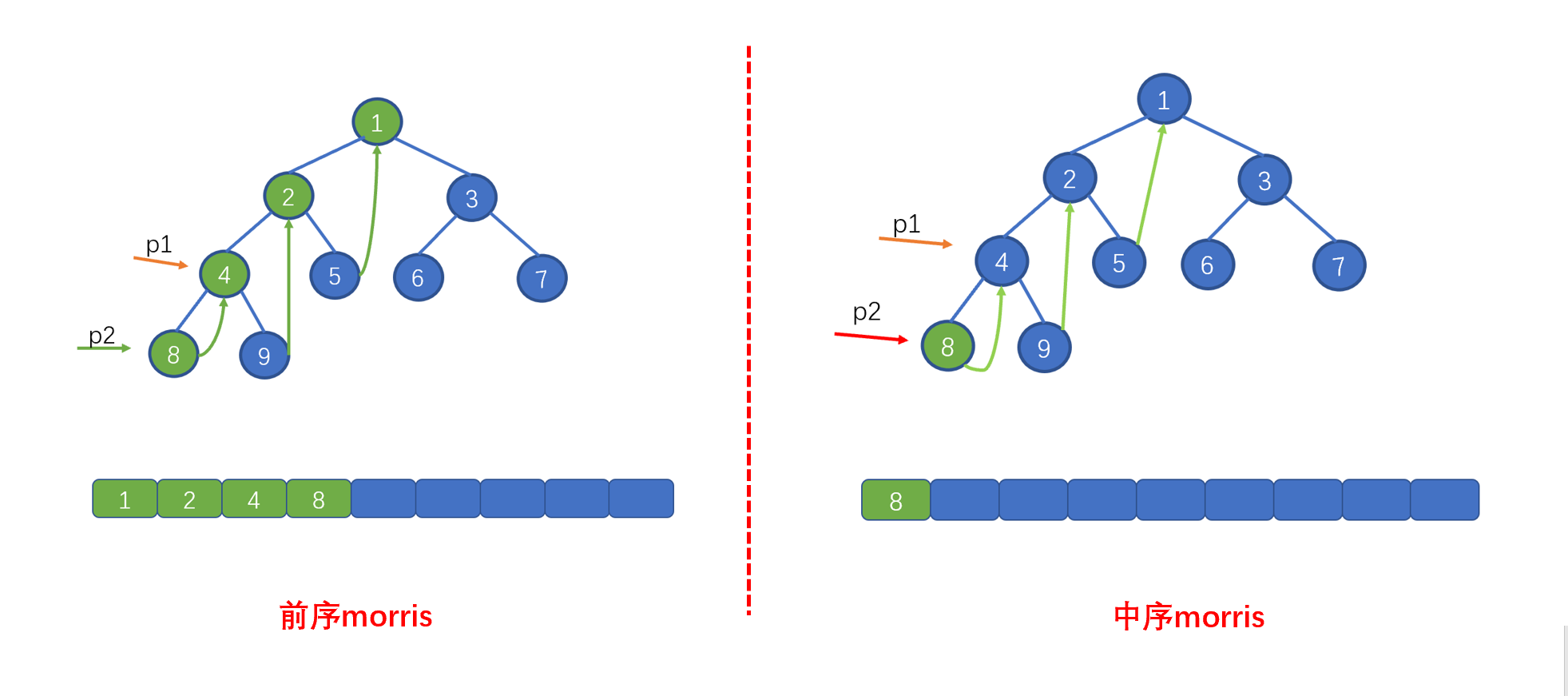
|
||||
|
||||
我们在前序遍历时,遇到 `p2.right == p1`的情况时,则会执行 `p2.right == null` 并让 `p1 = p1.right`,这样做是因为,我们此时 p1 指向的值已经遍历完毕,为了防止重复遍历。
|
||||
|
||||
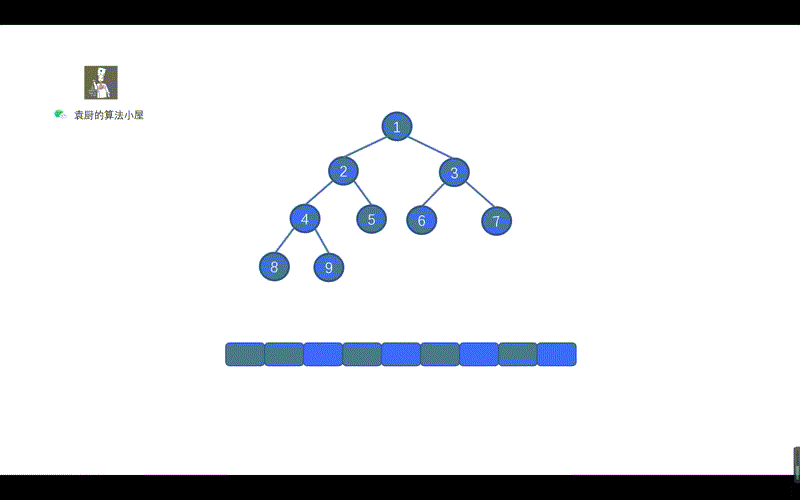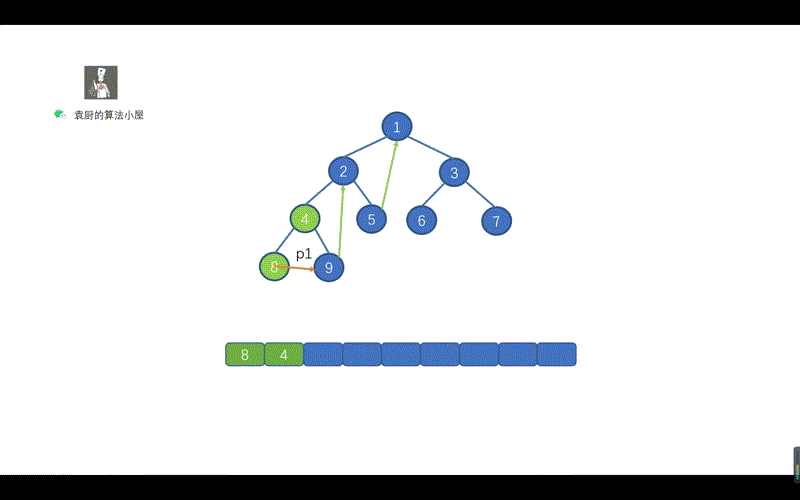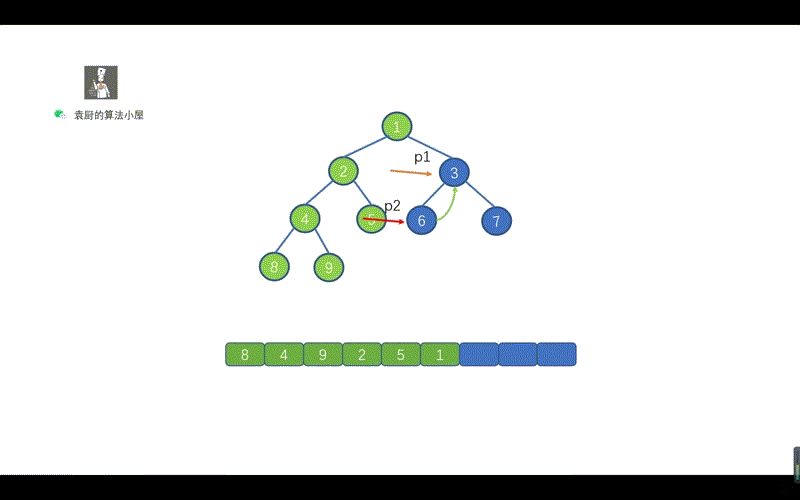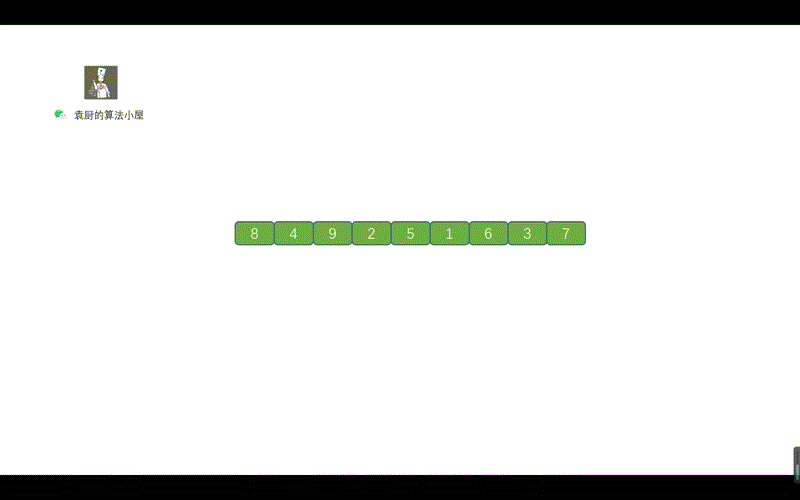
但是呢,在我们的中序 Morris 中我们遇到`p2.right == p1`此时 p1 还未遍历,所以我们需要在上面两条代码之间添加一行代码`list.add(p1.val);`
|
||||
|
||||
好啦,到这里我们就基本上就搞定了中序遍历的 Morris 方法,下面我们通过动画来加深一下印象吧,当然我也会把前序遍历的动画放在这里,大家可以看一下哪里有所不同。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
**参考代码:**
|
||||
|
||||
```java
|
||||
//中序 Morris
|
||||
class Solution {
|
||||
public List<Integer> inorderTraversal(TreeNode root) {
|
||||
List<Integer> list = new ArrayList<Integer>();
|
||||
if (root == null) {
|
||||
return list;
|
||||
}
|
||||
TreeNode p1 = root;
|
||||
TreeNode p2 = null;
|
||||
while (p1 != null) {
|
||||
p2 = p1.left;
|
||||
if (p2 != null) {
|
||||
while (p2.right != null && p2.right != p1) {
|
||||
p2 = p2.right;
|
||||
}
|
||||
if (p2.right == null) {
|
||||
p2.right = p1;
|
||||
p1 = p1.left;
|
||||
continue;
|
||||
} else {
|
||||
p2.right = null;
|
||||
}
|
||||
}
|
||||
list.add(p1.val);
|
||||
p1 = p1.right;
|
||||
}
|
||||
return list;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
@@ -37,7 +37,6 @@ PS:本篇文章内容较基础,对于没有学过数据结构的同学会有
|
||||
我们先来看下百度百科对树的定义
|
||||
|
||||
> 树是 n (n >= 0) 个节点的有限集。 n = 0 时 我们称之为空树, 空树是树的特例。
|
||||
>
|
||||
|
||||
在`任意一棵非空树`中:
|
||||
|
||||
|
||||
@@ -0,0 +1,106 @@
|
||||
### Morris
|
||||
|
||||
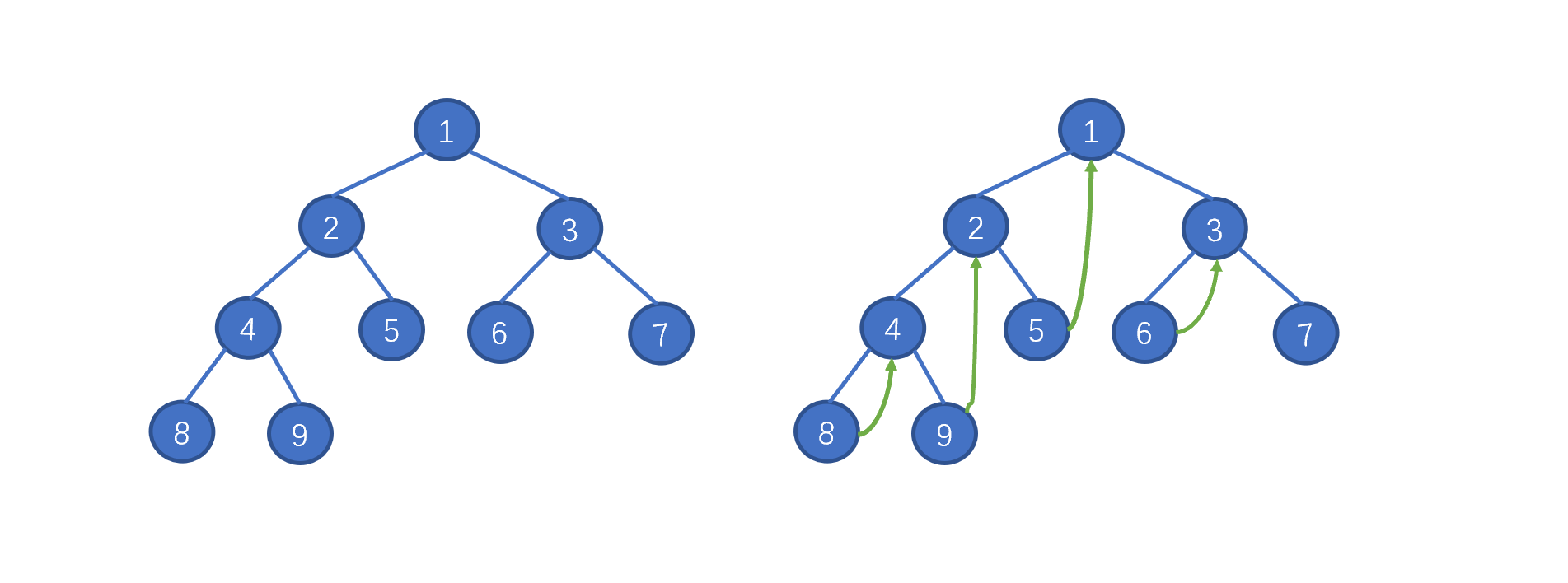
Morris 遍历利用树的左右孩子为空(大量空闲指针),实现空间开销的极限缩减。这个遍历方法,稍微有那么一丢丢难理解,不过结合动图,也就一目了然啦,下面我们先看动画吧。
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
看完视频,是不是感觉自己搞懂了,又感觉自己没搞懂,哈哈,咱们继续往下看。
|
||||
|
||||
|
||||
|
||||
我们之前说的,Morris 遍历利用了`树中大量空闲指针的特性`,我们需要`找到当前节点的左子树中的最右边的叶子节点`,将该叶子节点的 right 指向当前节点。例如当前节点为2,其左子树中的最右节点为 9 ,则在 9 节点添加一个 right 指针指向 2。
|
||||
|
||||
其实上图中的 Morris 遍历遵循两个原则,我们在动画中也能够得出。
|
||||
|
||||
1. 当 p1.left == null 时,p1 = p1.right。(这也就是我们为什么要给叶子节点添加 right 指针的原因)
|
||||
|
||||
2. 如果 p1.left != null,找到 p1 左子树上最右的节点。(也就是我们的 p2 最后停留的位置),此时我们又可以分为两种情况,一种是叶子节点添加 right 指针的情况,一种是去除叶子节点 right 指针的情况。
|
||||
|
||||
3. - 如果 p2 的 right 指针指向空,让其指向 p1,p1向左移动,即 p1 = p1.left
|
||||
- 如果 p2 的 right 指针指向 p1,让其指向空,(为了防止重复执行,则需要去掉 right 指针)p1 向右移动,p1 = p1.right。
|
||||
|
||||
这时你可以结合咱们刚才提到的两个原则,再去看一遍动画,并代入规则进行模拟,差不多就能完全搞懂啦。
|
||||
|
||||
下面我们来对动画中的内容进行拆解 ,
|
||||
|
||||
首先 p1 指向 root节点
|
||||
|
||||
p2 = p1.left,下面我们需要通过 p2 找到 p1的左子树中的最右节点。即节点 5,然后将该节点的 right 指针指向 root。并记录 root 节点的值。
|
||||
|
||||

|
||||
|
||||
向左移动 p1,即 p1 = p1.left
|
||||
|
||||
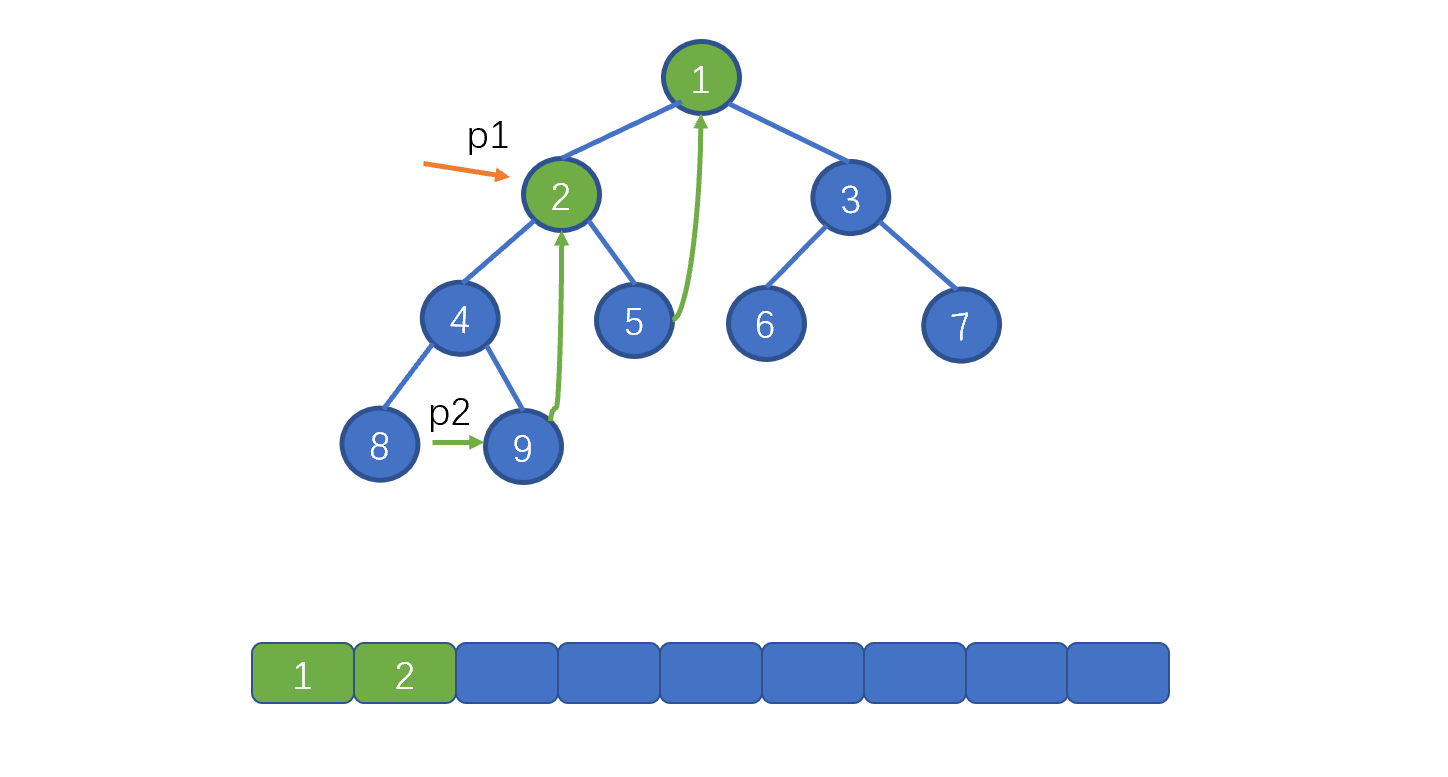
p2 = p1.left ,即节点 4 ,找到 p1 的左子树中的最右叶子节点,也就是 9,并将该节点的 right 指针指向 2。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
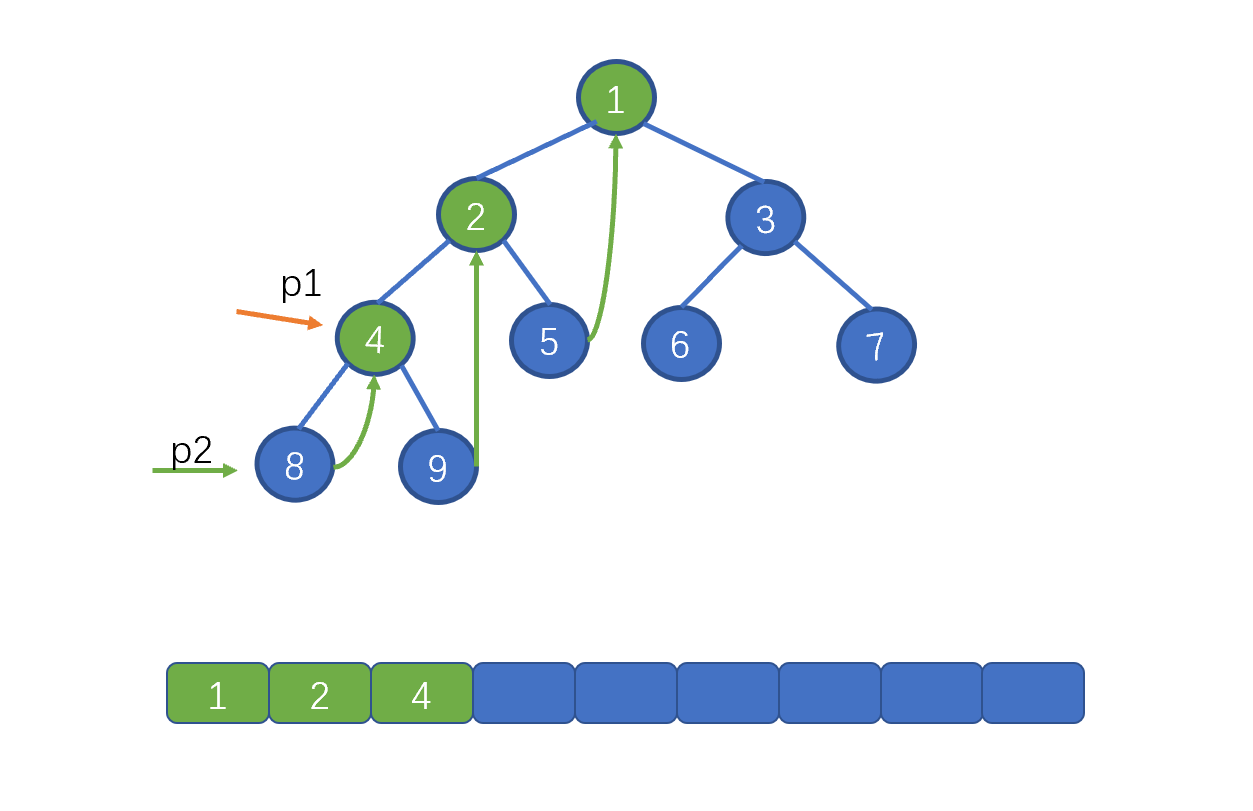
继续向左移动 p1,即 p1 = p1.left,p2 = p1.left。 也就是节点 8。并将该节点的 right 指针指向 p1。
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
我们发现这一步给前两步是一样的,都是找到叶子节点,将其 right 指针指向 p1,此时我们完成了添加 right 指针的过程,下面我们继续往下看。
|
||||
|
||||
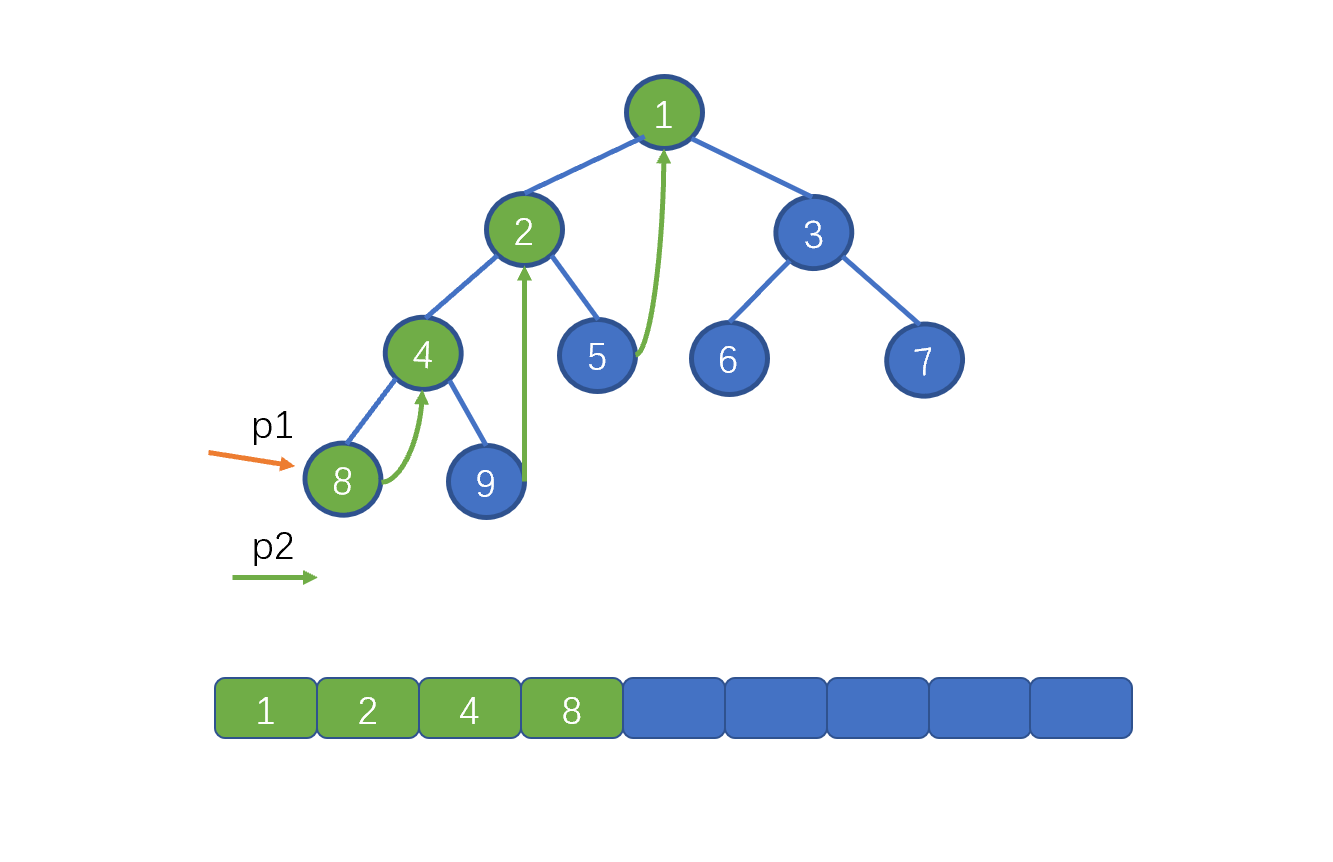
我们继续移动 p1 指针,p1 = p1.left。p2 = p.left。此时我们发现 p2 == null,即下图
|
||||
|
||||
|
||||
|
||||
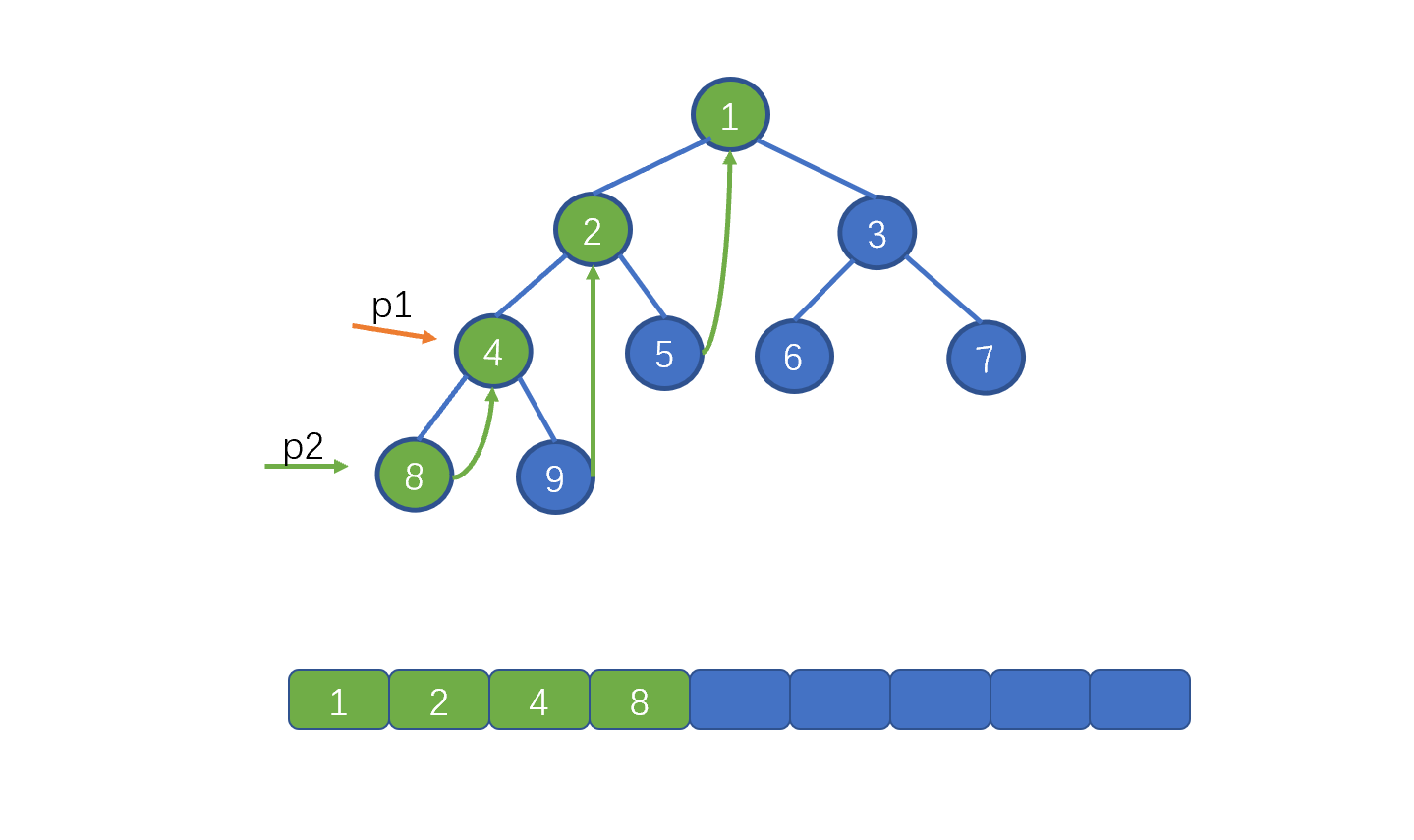
此时我们需要移动 p1, 但是不再是 p1 = p1.left 而是 p1 = p1.right。也就是 4,继续让 p2 = p1.left。此时则为下图这种情况
|
||||
|
||||
|
||||
|
||||
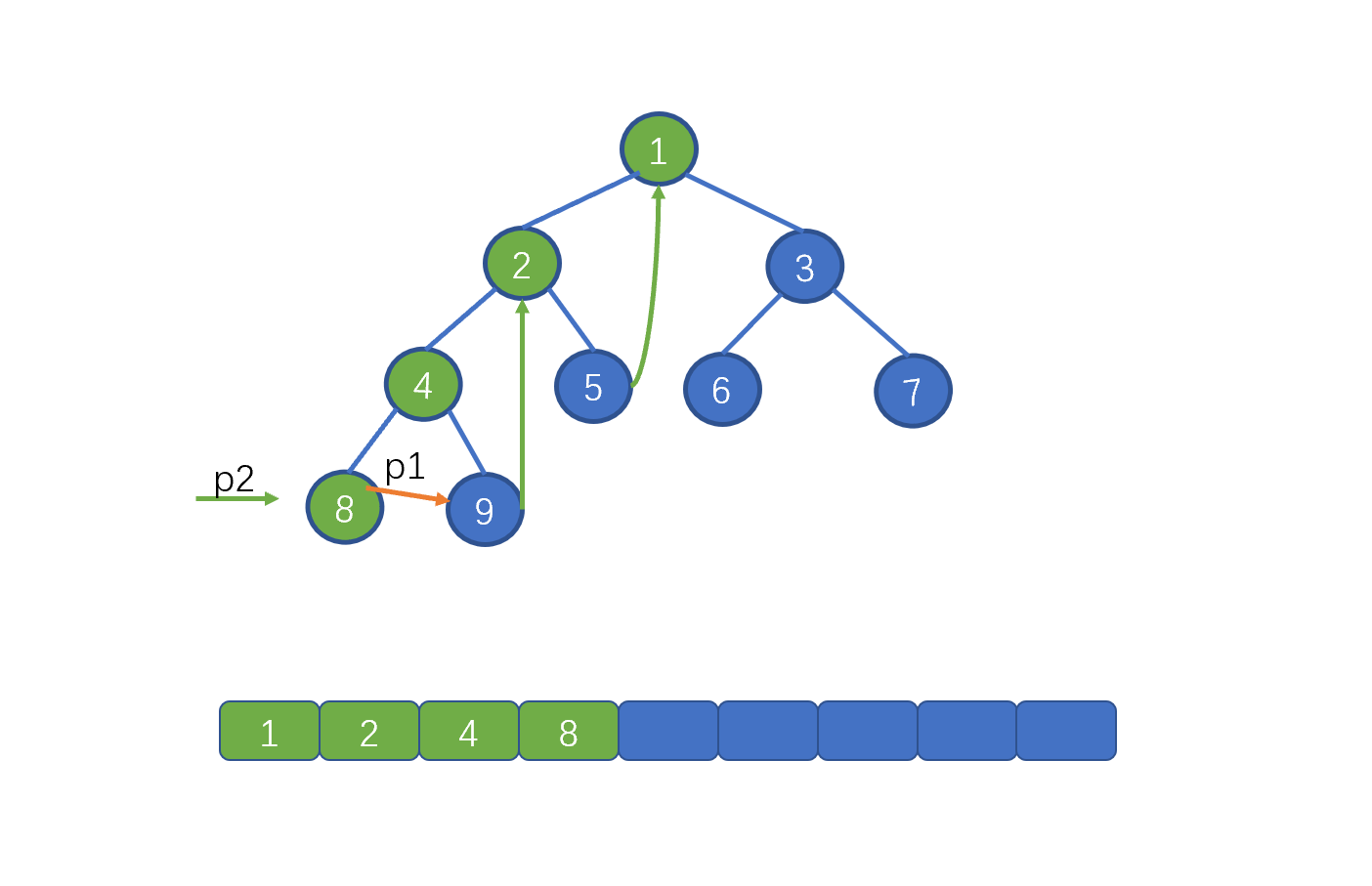
此时我们发现 p2.right != null 而是指向 4,说明此时我们已经添加过了 right 指针,所以去掉 right 指针,并让 p1 = p1.right
|
||||
|
||||
|
||||
|
||||
下面则继续移动 p1 ,按照规则继续移动即可,遇到的情况已经在上面做出了举例,所以下面我们就不继续赘述啦,如果还不是特别理解的同学,可以再去看一遍动画加深下印象。
|
||||
|
||||
时间复杂度 O(n),空间复杂度 O(1)
|
||||
|
||||
下面我们来看代码吧。
|
||||
|
||||
#### 代码
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public List<Integer> preorderTraversal(TreeNode root) {
|
||||
|
||||
List<Integer> list = new ArrayList<>();
|
||||
if (root == null) {
|
||||
return list;
|
||||
}
|
||||
TreeNode p1 = root; TreeNode p2 = null;
|
||||
while (p1 != null) {
|
||||
p2 = p1.left;
|
||||
if (p2 != null) {
|
||||
//找到左子树的最右叶子节点
|
||||
while (p2.right != null && p2.right != p1) {
|
||||
p2 = p2.right;
|
||||
}
|
||||
//添加 right 指针,对应 right 指针为 null 的情况
|
||||
if (p2.right == null) {
|
||||
list.add(p1.val);
|
||||
p2.right = p1;
|
||||
p1 = p1.left;
|
||||
continue;
|
||||
}
|
||||
//对应 right 指针存在的情况,则去掉 right 指针
|
||||
p2.right = null;
|
||||
} else {
|
||||
list.add(p1.val);
|
||||
}
|
||||
//移动 p1
|
||||
p1 = p1.right;
|
||||
}
|
||||
return list;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
好啦,今天就看到这里吧,咱们下期见!
|
||||
@@ -67,107 +67,3 @@ class Solution {
|
||||
}
|
||||
```
|
||||
|
||||
### Morris
|
||||
|
||||
Morris 遍历利用树的左右孩子为空(大量空闲指针),实现空间开销的极限缩减。这个遍历方法,稍微有那么一丢丢难理解,不过结合动图,也就一目了然啦,下面我们先看动画吧。
|
||||
|
||||
|
||||
|
||||
看完视频,是不是感觉自己搞懂了,又感觉自己没搞懂,哈哈,咱们继续往下看。
|
||||
|
||||

|
||||
|
||||
我们之前说的,Morris 遍历利用了`树中大量空闲指针的特性`,我们需要`找到当前节点的左子树中的最右边的叶子节点`,将该叶子节点的 right 指向当前节点。例如当前节点为2,其左子树中的最右节点为 9 ,则在 9 节点添加一个 right 指针指向 2。
|
||||
|
||||
其实上图中的 Morris 遍历遵循两个原则,我们在动画中也能够得出。
|
||||
|
||||
1. 当 p1.left == null 时,p1 = p1.right。(这也就是我们为什么要给叶子节点添加 right 指针的原因)
|
||||
|
||||
2. 如果 p1.left != null,找到 p1 左子树上最右的节点。(也就是我们的 p2 最后停留的位置),此时我们又可以分为两种情况,一种是叶子节点添加 right 指针的情况,一种是去除叶子节点 right 指针的情况。
|
||||
|
||||
3. - 如果 p2 的 right 指针指向空,让其指向 p1,p1向左移动,即 p1 = p1.left
|
||||
- 如果 p2 的 right 指针指向 p1,让其指向空,(为了防止重复执行,则需要去掉 right 指针)p1 向右移动,p1 = p1.right。
|
||||
|
||||
这时你可以结合咱们刚才提到的两个原则,再去看一遍动画,并代入规则进行模拟,差不多就能完全搞懂啦。
|
||||
|
||||
下面我们来对动画中的内容进行拆解 ,
|
||||
|
||||
首先 p1 指向 root节点
|
||||
|
||||
p2 = p1.left,下面我们需要通过 p2 找到 p1的左子树中的最右节点。即节点 5,然后将该节点的 right 指针指向 root。并记录 root 节点的值。
|
||||
|
||||

|
||||
|
||||
向左移动 p1,即 p1 = p1.left
|
||||
|
||||
p2 = p1.left ,即节点 4 ,找到 p1 的左子树中的最右叶子节点,也就是 9,并将该节点的 right 指针指向 2。
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
继续向左移动 p1,即 p1 = p1.left,p2 = p1.left。 也就是节点 8。并将该节点的 right 指针指向 p1。
|
||||
|
||||

|
||||
|
||||
|
||||
|
||||
我们发现这一步给前两步是一样的,都是找到叶子节点,将其 right 指针指向 p1,此时我们完成了添加 right 指针的过程,下面我们继续往下看。
|
||||
|
||||
我们继续移动 p1 指针,p1 = p1.left。p2 = p.left。此时我们发现 p2 == null,即下图
|
||||
|
||||

|
||||
|
||||
此时我们需要移动 p1, 但是不再是 p1 = p1.left 而是 p1 = p1.right。也就是 4,继续让 p2 = p1.left。此时则为下图这种情况
|
||||
|
||||

|
||||
|
||||
此时我们发现 p2.right != null 而是指向 4,说明此时我们已经添加过了 right 指针,所以去掉 right 指针,并让 p1 = p1.right
|
||||
|
||||

|
||||
|
||||
下面则继续移动 p1 ,按照规则继续移动即可,遇到的情况已经在上面做出了举例,所以下面我们就不继续赘述啦,如果还不是特别理解的同学,可以再去看一遍动画加深下印象。
|
||||
|
||||
时间复杂度 O(n),空间复杂度 O(1)
|
||||
|
||||
下面我们来看代码吧。
|
||||
|
||||
#### 代码
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public List<Integer> preorderTraversal(TreeNode root) {
|
||||
|
||||
List<Integer> list = new ArrayList<>();
|
||||
if (root == null) {
|
||||
return list;
|
||||
}
|
||||
TreeNode p1 = root; TreeNode p2 = null;
|
||||
while (p1 != null) {
|
||||
p2 = p1.left;
|
||||
if (p2 != null) {
|
||||
//找到左子树的最右叶子节点
|
||||
while (p2.right != null && p2.right != p1) {
|
||||
p2 = p2.right;
|
||||
}
|
||||
//添加 right 指针,对应 right 指针为 null 的情况
|
||||
if (p2.right == null) {
|
||||
list.add(p1.val);
|
||||
p2.right = p1;
|
||||
p1 = p1.left;
|
||||
continue;
|
||||
}
|
||||
//对应 right 指针存在的情况,则去掉 right 指针
|
||||
p2.right = null;
|
||||
} else {
|
||||
list.add(p1.val);
|
||||
}
|
||||
//移动 p1
|
||||
p1 = p1.right;
|
||||
}
|
||||
return list;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
好啦,今天就看到这里吧,咱们下期见!
|
||||
207
animation-simulation/二叉树/二叉树的后续遍历.md
Normal file
207
animation-simulation/二叉树/二叉树的后续遍历.md
Normal file
@@ -0,0 +1,207 @@
|
||||
之前给大家介绍了二叉树的[前序遍历](),[中序遍历]()的迭代法和 Morris 方法,今天咱们来说一下二叉后序遍历的迭代法及 Morris 方法。
|
||||
|
||||
注:阅读该文章前,建议各位先阅读之前的三篇文章,对该文章的理解有很大帮助。
|
||||
|
||||
## 迭代
|
||||
|
||||
后序遍历的相比前两种方法,难理解了一些,所以这里我们需要认真思考一下,每一行的代码的作用。
|
||||
|
||||
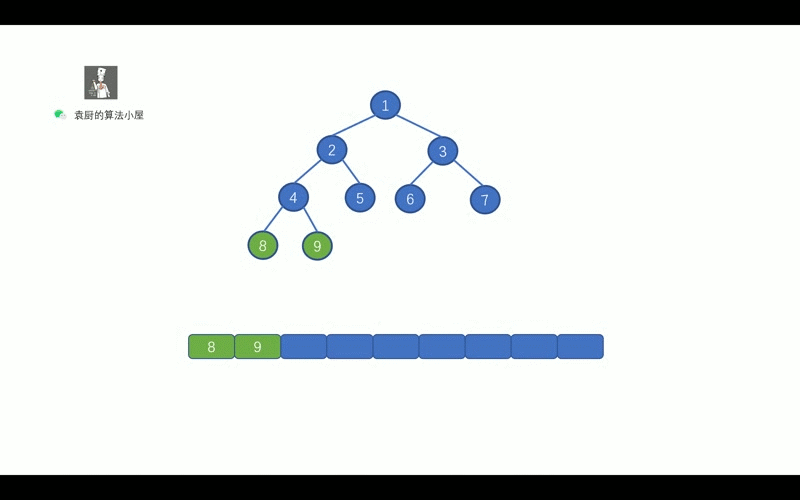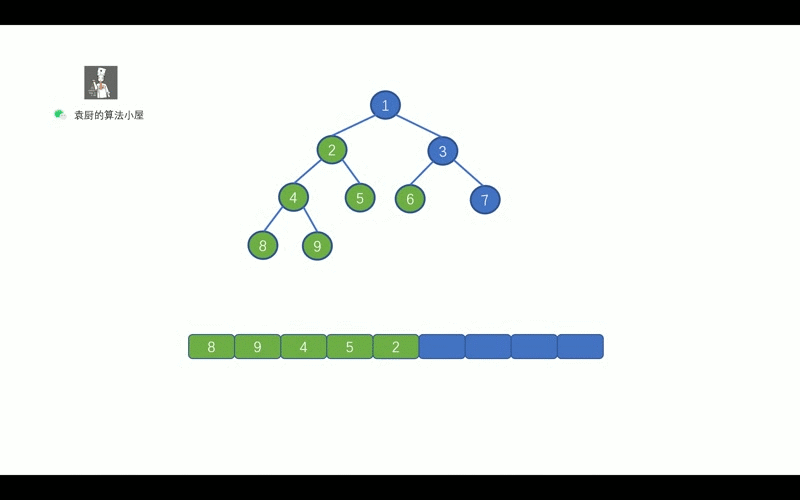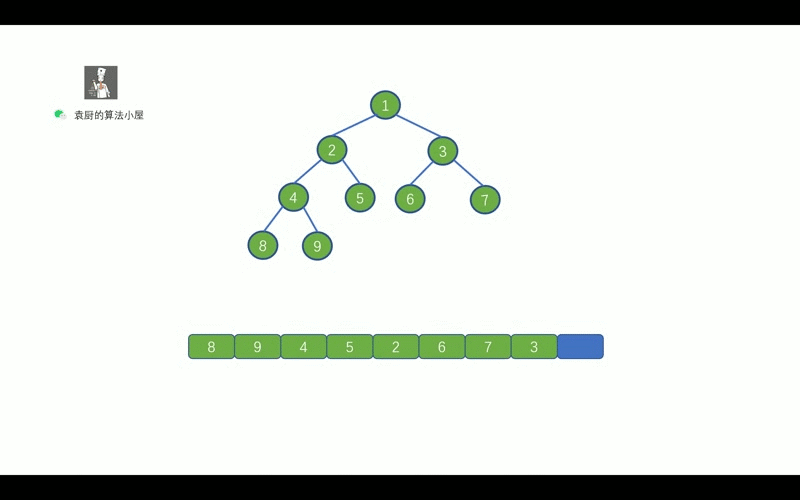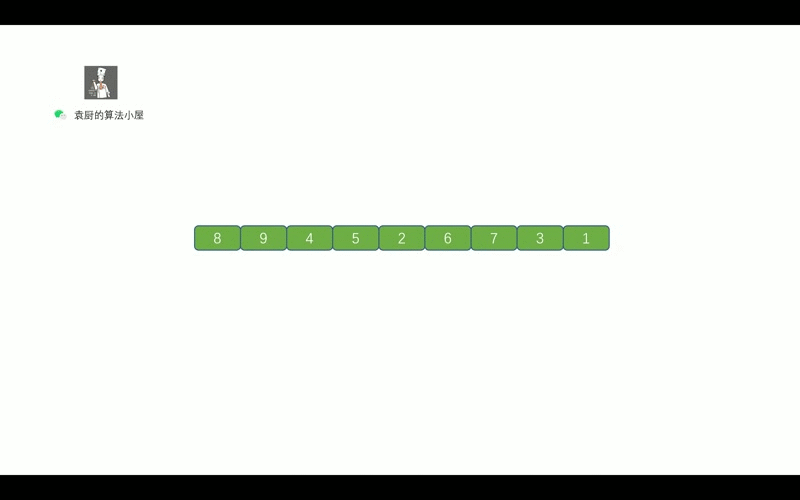
我们先来复习一下,二叉树的后序遍历
|
||||
|
||||
|
||||
|
||||
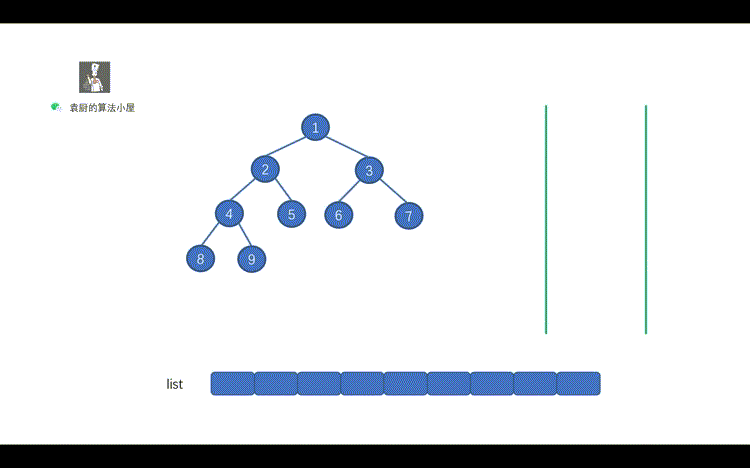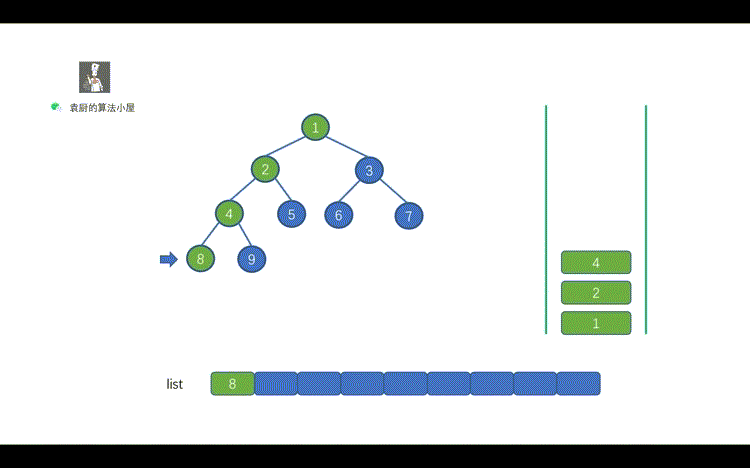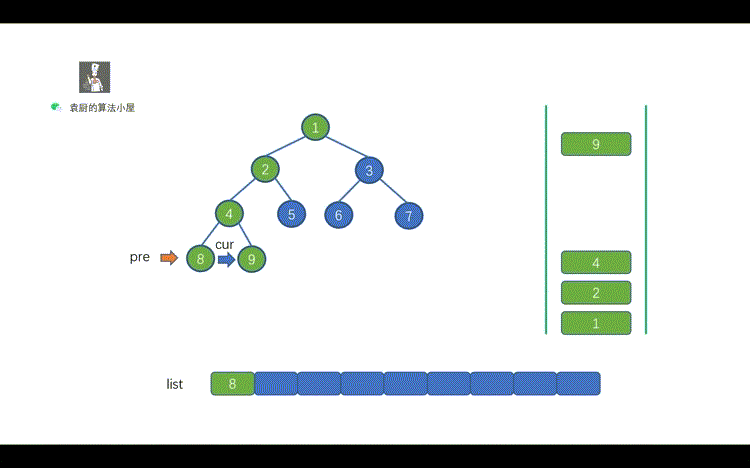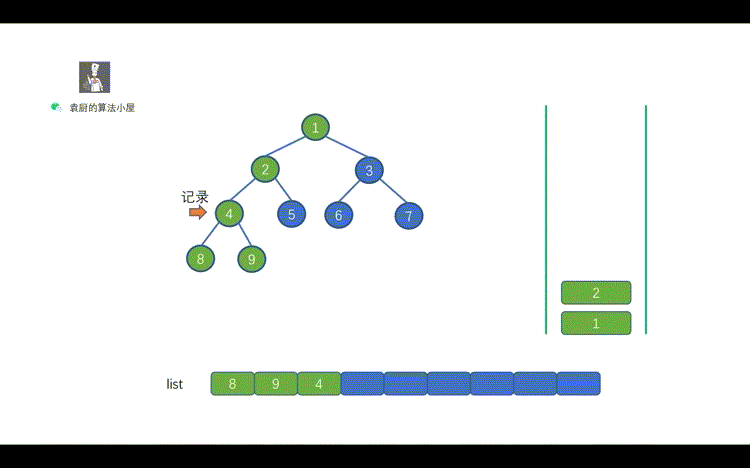
我们知道后序遍历的顺序是,` 对于树中的某节点, 先遍历该节点的左子树, 再遍历其右子树, 最后遍历该节点`。
|
||||
|
||||
那么我们如何利用栈来解决呢?
|
||||
|
||||
我们直接来看动画,看动画之前,但是我们`需要带着问题看动画`,问题搞懂之后也就搞定了后序遍历。
|
||||
|
||||
1.动画中的橙色指针发挥了什么作用
|
||||
|
||||
2.为什么动画中的某节点,为什么出栈后又入栈呢?
|
||||
|
||||
好啦,下面我们看动画吧!
|
||||
|
||||
|
||||
|
||||
相信大家看完动画之后,也能够发现其中规律。
|
||||
|
||||
我们来对其中之前提出的问题进行解答
|
||||
|
||||
1.动画中的橙色箭头的作用?
|
||||
|
||||
> 用来定位住上一个访问节点,这样我们就知道 cur 节点的 right 节点是否被访问,如果被访问,我们则需要遍历 cur 节点。
|
||||
|
||||
2.为什么有的节点出栈后又入栈了呢?
|
||||
|
||||
> 出栈又入栈的原因是,我们发现 cur 节点的 right 不为 null ,并且 cur.right 也没有被访问过。因为 `cur.right != preNode `,所以当前我们还不能够遍历该节点,应该先遍历其右子树中的节点。
|
||||
>
|
||||
> 所以我们将其入栈后,然后`cur = cur.right`
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
public List<Integer> postorderTraversal(TreeNode root) {
|
||||
Stack<TreeNode> stack = new Stack<>();
|
||||
List<Integer> list = new ArrayList<>();
|
||||
TreeNode cur = root;
|
||||
//这个用来记录前一个访问的节点,也就是橙色箭头
|
||||
TreeNode preNode = null;
|
||||
while (cur != null || !stack.isEmpty()) {
|
||||
//和之前写的中序一致
|
||||
while (cur != null) {
|
||||
stack.push(cur);
|
||||
cur = cur.left;
|
||||
}
|
||||
//1.出栈,可以想一下,这一步的原因。
|
||||
cur = stack.pop();
|
||||
//2.if 里的判断语句有什么含义?
|
||||
if (cur.right == null || cur.right == preNode) {
|
||||
list.add(cur.val);
|
||||
//更新下 preNode,也就是定位住上一个访问节点。
|
||||
preNode = cur;
|
||||
cur = null;
|
||||
} else {
|
||||
//3.再次压入栈,和上面那条 1 的关系?
|
||||
stack.push(cur);
|
||||
cur = cur.right;
|
||||
}
|
||||
}
|
||||
return list;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
当然也可以修改下代码逻辑将 `cur = stack.pop()` 改成 `cur = stack.peek()`,下面再修改一两行代码也可以实现,这里这样写是方便动画模拟,大家可以随意发挥。
|
||||
|
||||
时间复杂度 O(n), 空间复杂度O(n)
|
||||
|
||||
这里二叉树的三种迭代方式到这里就结束啦,大家可以进行归纳总结,三种遍历方式大同小异,建议各位,掌握之后,自己手撕一下,从搭建二叉树开始。
|
||||
|
||||
另外大家也可以看下 Carl 哥的这篇文章,迭代遍历的另一种实现方式。
|
||||
|
||||
> https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/bang-ni-dui-er-cha-shu-bu-zai-mi-mang-che-di-chi-t/
|
||||
|
||||
好啦,下面我们看下后序遍历的 Morris 方法。
|
||||
|
||||
## Morris
|
||||
|
||||
后序遍历的 Morris 方法也比之前两种代码稍微长一些,看着挺唬人,其实不难,和我们之前说的没差多少。下面我们一起来干掉它吧。
|
||||
|
||||
我们先来复习下之前说过的[中序遍历](),见下图。
|
||||
|
||||

|
||||
|
||||
另外我们来对比下,中序遍历和后序遍历的 Morris 方法,代码有哪里不同。
|
||||
|
||||

|
||||
|
||||
由上图可知,仅仅有三处不同,后序遍历里少了 `list.add()`,多了一个函数` postMorris() ` ,那后序遍历的 list.add() 肯定是在 postMorris 函数中的。所以我们搞懂了 postMorris 函数,也就搞懂了后序遍历的 Morris 方法(默认大家看了之前的文章,没有看过的同学,可以点击文首的链接)
|
||||
|
||||
下面我们一起来剖析下 postMorris 函数.代码如下
|
||||
|
||||
```java
|
||||
public void postMorris(TreeNode root) {
|
||||
//反转转链表,详情看下方图片
|
||||
TreeNode reverseNode = reverseList(root);
|
||||
//遍历链表
|
||||
TreeNode cur = reverseNode;
|
||||
while (cur != null) {
|
||||
list.add(cur.val);
|
||||
cur = cur.right;
|
||||
}
|
||||
//反转回来
|
||||
reverseList(reverseNode);
|
||||
}
|
||||
|
||||
//反转链表
|
||||
public TreeNode reverseList(TreeNode head) {
|
||||
TreeNode cur = head;
|
||||
TreeNode pre = null;
|
||||
while (cur != null) {
|
||||
TreeNode next = cur.right;
|
||||
cur.right = pre;
|
||||
pre = cur;
|
||||
cur = next;
|
||||
}
|
||||
return pre;
|
||||
}
|
||||
```
|
||||
|
||||
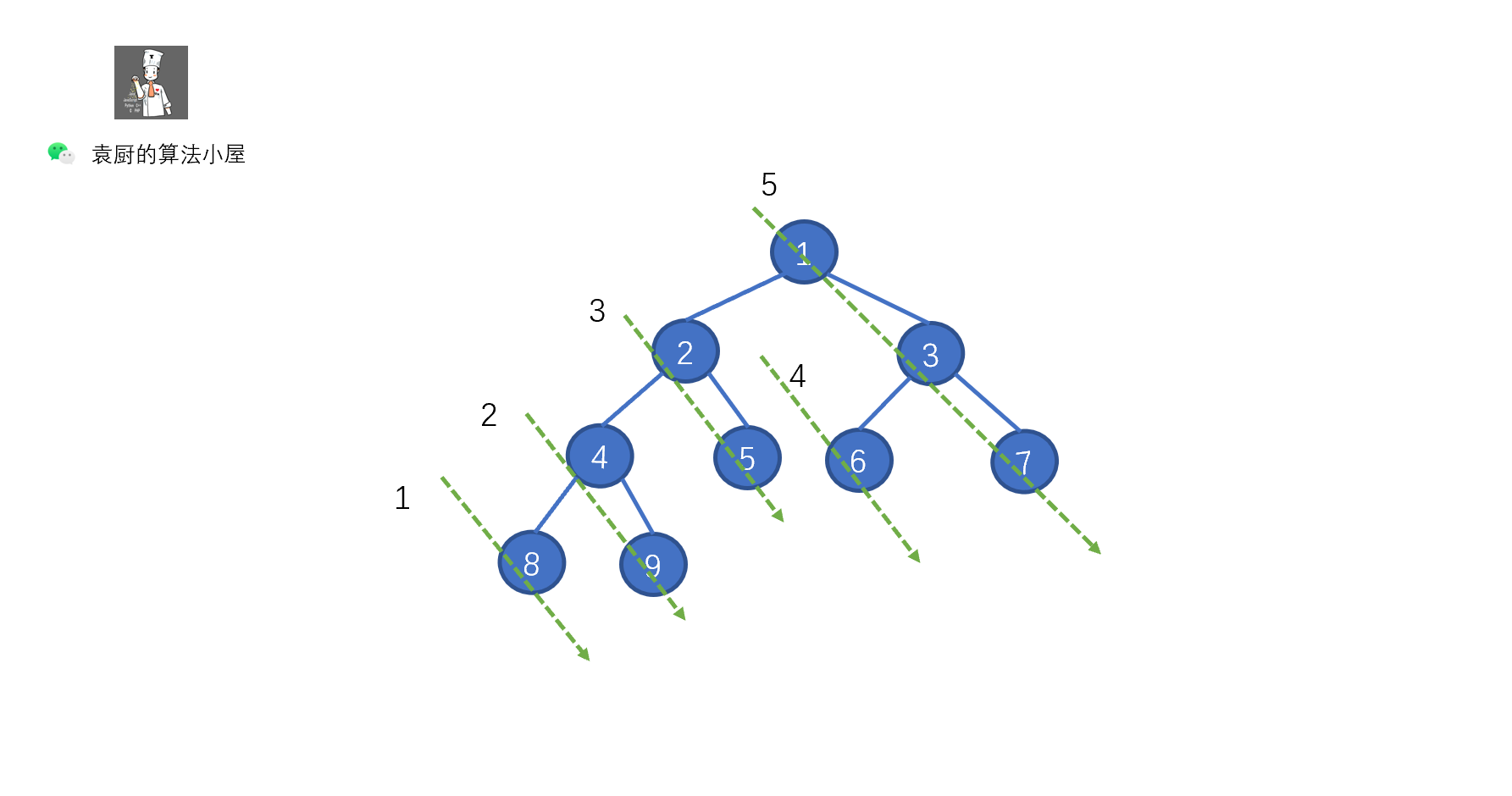
上面的代码,是不是贼熟悉,和我们的倒序输出链表一致,步骤为,反转链表,遍历链表,将链表反转回原样。只不过我们将 ListNode.next 写成了 TreeNode.right 将树中的遍历右子节点的路线,看成了一个链表,见下图。
|
||||
|
||||
|
||||
|
||||
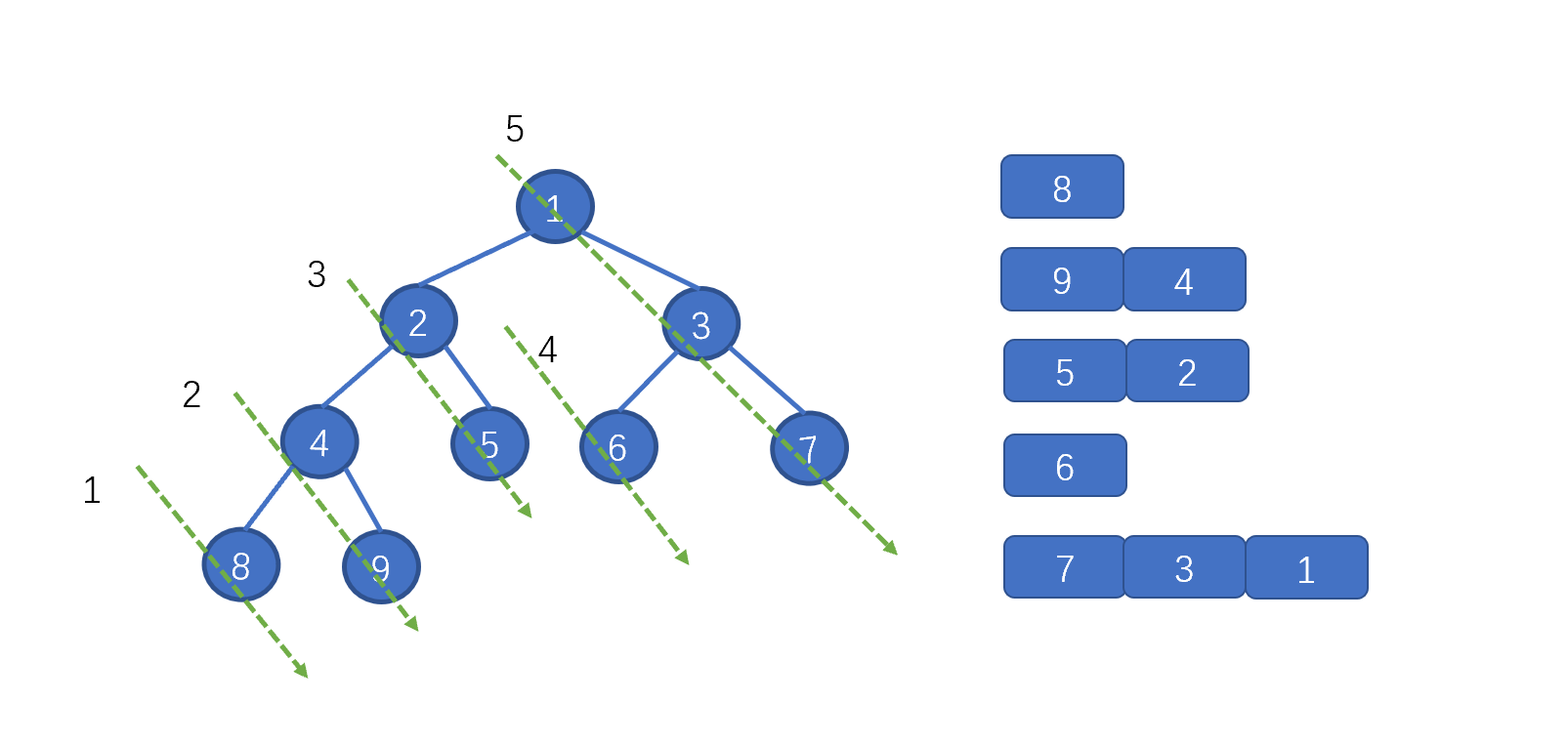
上图中的一个绿色虚线,代表一个链表,我们根据序号进行倒序遍历,看下是什么情况
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
到这块是不是就整懂啦,打完收工!
|
||||
|
||||
```java
|
||||
class Solution {
|
||||
List<Integer> list;
|
||||
public List<Integer> postorderTraversal(TreeNode root) {
|
||||
list = new ArrayList<>();
|
||||
if (root == null) {
|
||||
return list;
|
||||
}
|
||||
TreeNode p1 = root;
|
||||
TreeNode p2 = null;
|
||||
while (p1 != null) {
|
||||
p2 = p1.left;
|
||||
if (p2 != null) {
|
||||
while (p2.right != null && p2.right != p1) {
|
||||
p2 = p2.right;
|
||||
}
|
||||
if (p2.right == null) {
|
||||
p2.right = p1;
|
||||
p1 = p1.left;
|
||||
continue;
|
||||
} else {
|
||||
p2.right = null;
|
||||
postMorris(p1.left);
|
||||
}
|
||||
}
|
||||
p1 = p1.right;
|
||||
}
|
||||
//以根节点为起点的链表
|
||||
postMorris(root);
|
||||
return list;
|
||||
}
|
||||
public void postMorris(TreeNode root) {
|
||||
//翻转链表
|
||||
TreeNode reverseNode = reverseList(root);
|
||||
//从后往前遍历
|
||||
TreeNode cur = reverseNode;
|
||||
while (cur != null) {
|
||||
list.add(cur.val);
|
||||
cur = cur.right;
|
||||
}
|
||||
//翻转回来
|
||||
reverseList(reverseNode);
|
||||
}
|
||||
public TreeNode reverseList(TreeNode head) {
|
||||
TreeNode cur = head;
|
||||
TreeNode pre = null;
|
||||
while (cur != null) {
|
||||
TreeNode next = cur.right;
|
||||
cur.right = pre;
|
||||
pre = cur;
|
||||
cur = next;
|
||||
}
|
||||
return pre;
|
||||
}
|
||||
|
||||
}
|
||||
```
|
||||
|
||||
时间复杂度 O(n)空间复杂度 O(1)
|
||||
|
||||
总结:后序遍历比起前序和中序稍微复杂了一些,所以我们解题的时候,需要好好注意一下,迭代法的核心是利用一个指针来定位我们上一个遍历的节点,Morris 的核心是,将某节点的右子节点,看成是一条链表,进行反向遍历。
|
||||
|
||||
好啦,今天就唠到这吧,拜了个拜。
|
||||
|
||||
|
||||
|
||||
@@ -1,4 +0,0 @@
|
||||
$$
|
||||
ED = arg\quad max
|
||||
$$
|
||||
|
||||
Reference in New Issue
Block a user