9.0 KiB
如果阅读时,发现错误,或者动画不可以显示的问题可以添加我微信好友 tan45du_one ,备注 github + 题目 + 问题 向我反馈
感谢支持,该仓库会一直维护,希望对各位有一丢丢帮助。
另外希望手机阅读的同学可以来我的 公众号:袁厨的算法小屋 两个平台同步,想要和题友一起刷题,互相监督的同学,可以在我的小屋点击刷题小队进入。
137. 只出现一次的数字 II
给定一个非空整数数组,除了某个元素只出现一次以外,其余每个元素均出现了三次。找出那个只出现了一次的元素。
示例 1:
输入: [2,2,3,2] 输出: 3
示例 2:
输入: [0,1,0,1,0,1,99] 输出: 99
题目很容易理解,刚才的题目是其他元素出现两次,目标元素出现一次,该题是其他元素出现三次,目标元素出现一次,所以我们完全可以借助上题的一些做法解决该题。
求和法
解析
我们在上题中介绍了求和法的解题步骤,现在该题中其他元素都出现三次,我们的目标元素出现一次,所以我们利用求和法也是完全 OK 的。下面我们来看具体步骤吧。
1.通过遍历数组获取所有元素的和以及 HashSet 内元素的和。
2.(SumSet * 3 - SumNum)/ 2 即可,除以 2 是因为我们减去之后得到的是 2 倍的目标元素。
注:这个题目中需要注意溢出的情况 。
题目代码
Java Code:
class Solution {
public int singleNumber(int[] nums) {
HashSet<Integer> set = new HashSet<>();
long setsum = 0;
long numsum = 0;
for (int x : nums) {
//所有元素的和
numsum += x;
if (!set.contains(x)) {
//HashSet元素和
setsum += x;
}
set.add(x);
}
//返回只出现一次的数
return (int)((3 * setsum - numsum) / 2);
}
}
C++ Code:
class Solution {
public:
int singleNumber(vector<int>& nums) {
unordered_set<int> set;
long setsum = 0;
long numsum = 0;
for (int x : nums) {
//所有元素的和
numsum += x;
if (set.find(x) == set.end()) {
//HashSet内元素的和
setsum += x;
}
set.insert(x);
}
//返回值
return (3 * setsum - numsum) / 2;
}
};
JS Code:
var singleNumber = function(nums) {
let set = new Set();
let setsum = 0;
let numsum = 0;
for (let x of nums) {
//所有元素的和
numsum += x;
if (!set.has(x)) {
setsum += x;
}
//HashSet内元素的和
set.add(x);
}
//返回值
return (3 * setsum - numsum) / 2;
};
Python Code:
class Solution:
def singleNumber(self, nums: List[int]) -> int:
return (3 * sum(set(nums)) - sum(nums)) // 2
这个题目用 HashMap 和排序查找肯定也是可以的,大家可以自己写一下,另外我们在第一题中有个利用异或求解的方法,但是这个题目是出现三次,我们则不能利用直接异或来求解,那还有其他方法吗?
位运算
解析
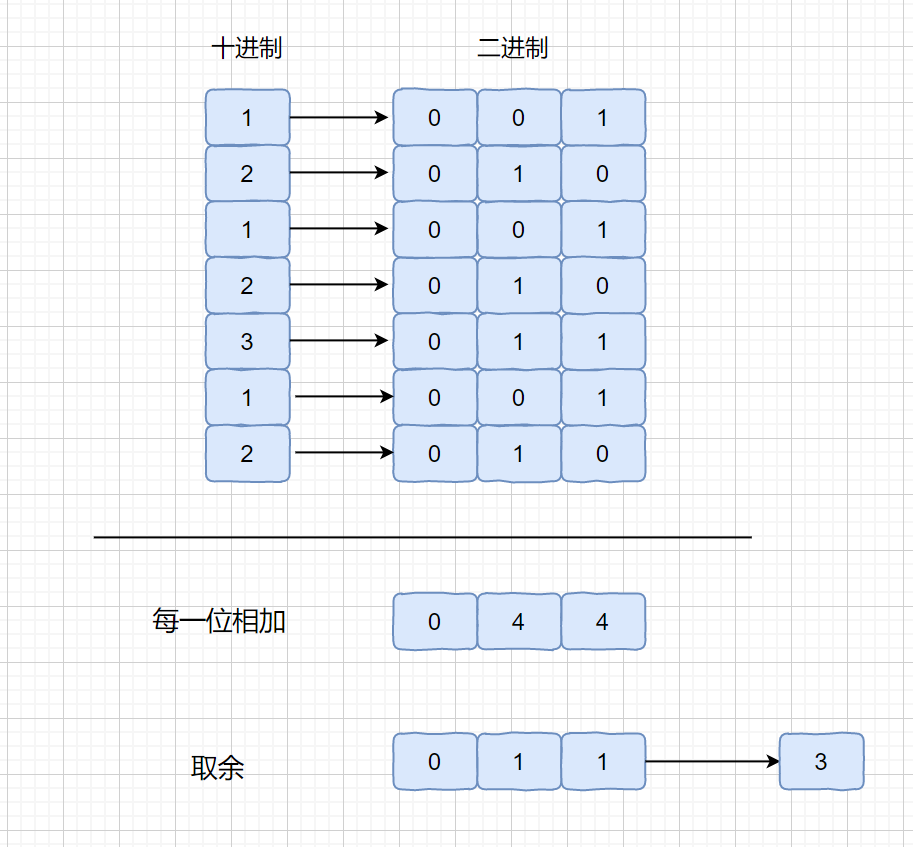
这个方法主要做法是将我们的数的二进制位每一位相加,然后对其每一位的和与 3 取余 ,我们看下面的例子。
那么我们为什么要这样做呢?大家想一下,如果其他数都出现 3 次,只有目标数出现 1 次,那么每一位的 1 的个数无非有这两种情况,为 3 的倍数(全为出现三次的数)或 3 的倍数 +1(包含出现一次的数)。这个 3 的倍数 +1 的情况也就是我们的目标数的那一位。
题目代码
Java Code:
class Solution {
public int singleNumber(int[] nums) {
int res = 0;
for(int i = 0; i < 32; i++){
int count = 0;
for (int num: nums) {
//检查第 i 位是否为 1
if ((num >> i & 1) == 1) {
count++;
}
}
if (count % 3 != 0) {
// 将第 i 位设为 1
res = res | 1 << i;
}
}
return res;
}
}
C++ Code:
class Solution {
public:
int singleNumber(vector<int>& nums) {
int res = 0;
for(int i = 0; i < 32; i++){
int count = 0;
for (int num: nums) {
//检查第 i 位是否为 1
if ((num >> i & 1) == 1) {
count++;
}
}
if (count % 3 != 0) {
// 将第 i 位设为 1
res = res | 1 << i;
}
}
return res;
}
};
JS Code:
var singleNumber = function(nums) {
let res = 0;
for(let i = 0; i < 32; i++){
let count = 0;
for (let num of nums) {
//检查第 i 位是否为 1
if ((num >> i & 1) == 1) {
count++;
}
}
if (count % 3 != 0) {
// 将第 i 位设为 1
res = res | 1 << i;
}
}
return res;
};
Python Code:
class Solution:
def singleNumber(self, nums: List[int]) -> int:
res = 0
for i in range(32):
count = 0
for num in nums:
# 检查第 i 位是否为 1
if (num >> i & 1) == 1:
count += 1
if count % 3 != 0:
# 将第 i 位设为 1
res = res | 1 << i
# 这里的做法稍有不同,见下方解释
if (res >> 31 & 1) == 1:
res = ~(res ^ 4294967295)
return res
我们来解析一下我们的代码:
<< 左移运算符:运算数的各二进位全部左移若干位,由 << 右边的数字指定了移动的位数,高位丢弃,低位补0。
>> 右移运算符:>> ** 左边的运算数的各二进位全部右移若干位,>>** 右边的数字指定了移动的位数。
另外我们的代码中还包含了 a & 1 和 a | 1 这有什么作用呢?继续看下图。
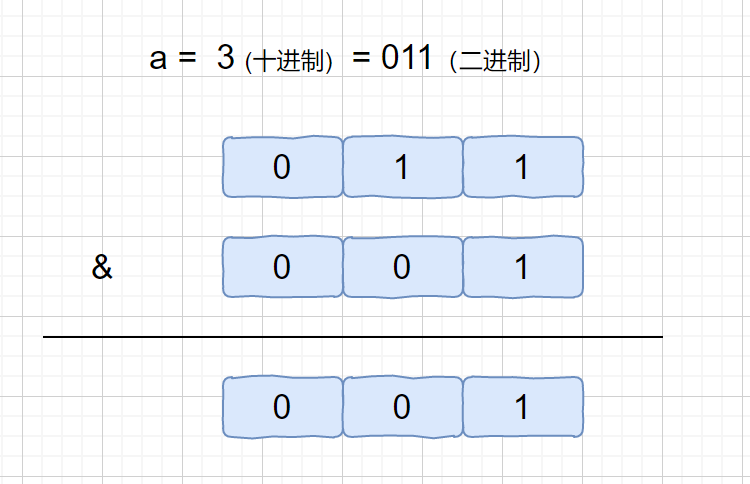
& 按位与运算符:参与运算的两个值,如果两个相应位都为1,则该位的结果为1,否则为0。
因为我们 a & 1 中 1 只有最后一位为 1,其余位皆为 0 ,所以我们发现 a & 1 的作用就是判断 a 的最后一位是否为 1 ,如果 a 的最后一位为 1 ,a & 1 = 1,否则为 0 。所以我们还可以通过这个公式来判断 a 的奇偶性。
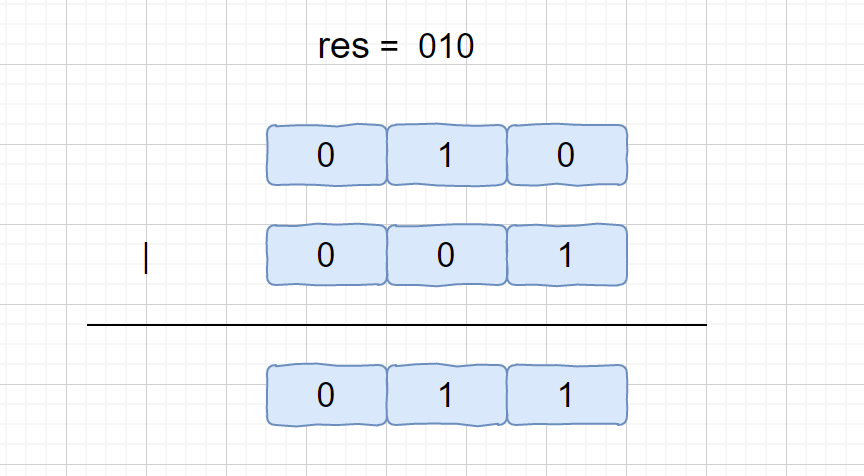
| 按位或运算符:只要对应的二个二进位有一个为1时,结果位就为1。
这个公式的作用就是将我们移位后的 res 的最后一位 0 变为 1。这个 1 也就代表着我们只出现一次元素的某一位。
贡献者@jaredliw注:
这里我想解释一下 python 里的这两行:
if (res >> 31 & 1) == 1: res = ~(res ^ 4294967295)int 的的符号是由最高位(这题用的是32位)的值决定,1 就是负数,0就是正数。由于 python 的 int 类型理论上是无限大的,这题里的 res 都会被认定为是正数。举个例子,32位的 -4 是这样的:
11111111111111111111111111111100 (最高位是 1 )= -4
python 里的则是这样的:
...000000000000 11111111111111111111111111111100 (前面跟着无限个 0,最高位是 0 )= 4294967292
怎么办呢?
我们可以先将 res 的后32位取反(与 4294967295 异或,4294967295 的二进制是 32 个 1),得到:
...000000000000 00000000000000000000000000000011(最高位是0)= 3
之后再用波浪号按位取反,得到:
...111111111111 11111111111111111111111111111100 (前面跟着无限个 1,最高位是 1)= -4
大家可以自行验证看看:
(res >> n & 1) == 1,n 随便填个大于 31 的数字,之前是 false,之后就变成 true (代表第 33 位,第 34 位,……都转成 1 了)。虽然说这种方法有一种脱裤子放屁的感觉 ,而且
res -= 2 ** 32也能办到,但由于涉及到 int 存储的问题(我省略了许多,大家自行度娘哈),我觉得还是有必要知道的。