mirror of
https://github.com/chefyuan/algorithm-base.git
synced 2024-11-19 18:43:38 +00:00
158 lines
6.1 KiB
Java
158 lines
6.1 KiB
Java
哈喽大家好,我是厨子,之前我们说了二叉树前序遍历的迭代法和 Morris,今天咱们写一下中序遍历的迭代法和 Morris。
|
||
|
||
> 注:数据结构掌握不熟练的同学,阅读该文章之前,可以先阅读这两篇文章,二叉树基础,前序遍历另外喜欢电脑阅读的同学,可以在小屋后台回复仓库地址,获取 Github 链接进行阅读。
|
||
|
||
中序遍历的顺序是, `对于树中的某节点,先遍历该节点的左子树, 然后再遍历该节点, 最后遍历其右子树`。老规矩,上动画,我们先通过动画回忆一下二叉树的中序遍历。
|
||
|
||
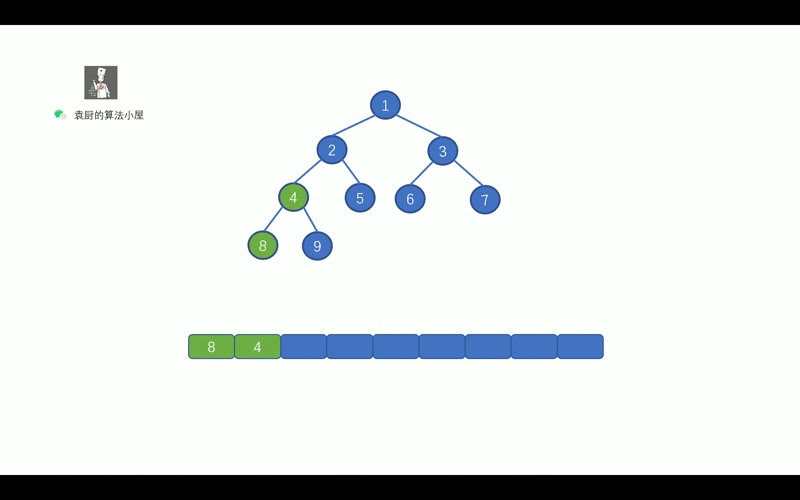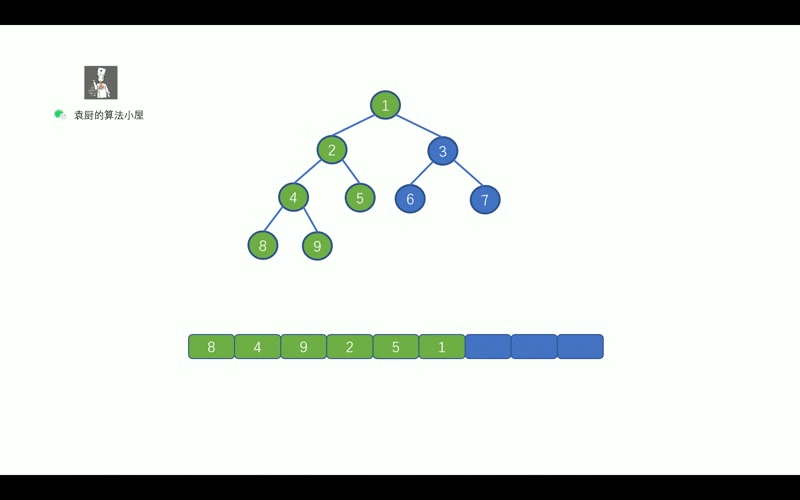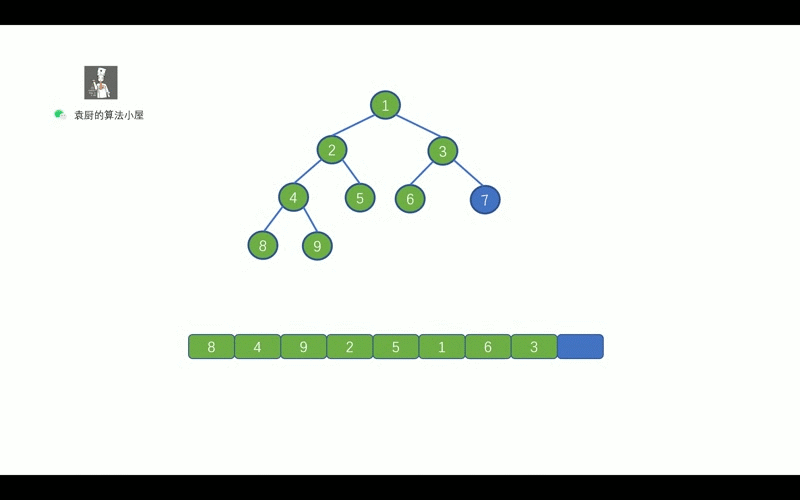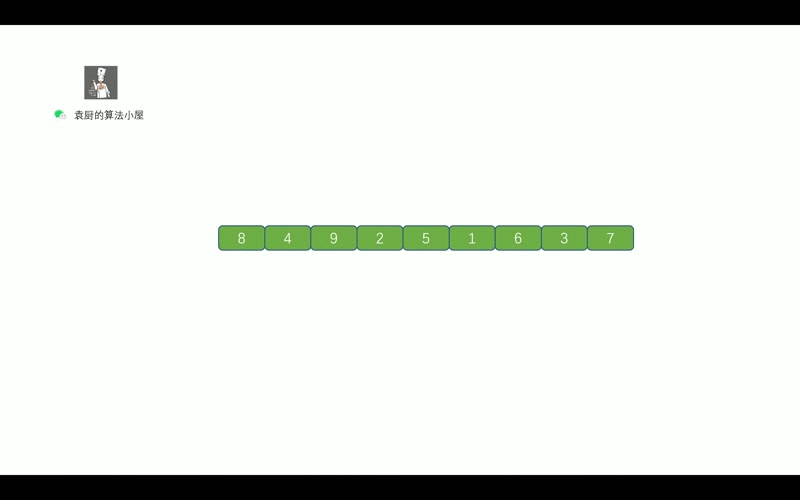
|
||
|
||
注:二叉树基础总结大家可以阅读这篇文章,点我。
|
||
|
||
## 迭代法
|
||
|
||
我们二叉树的中序遍历迭代法和前序遍历是一样的,都是借助栈来帮助我们完成。
|
||
|
||
我们结合动画思考一下,该如何借助栈来实现呢?
|
||
|
||
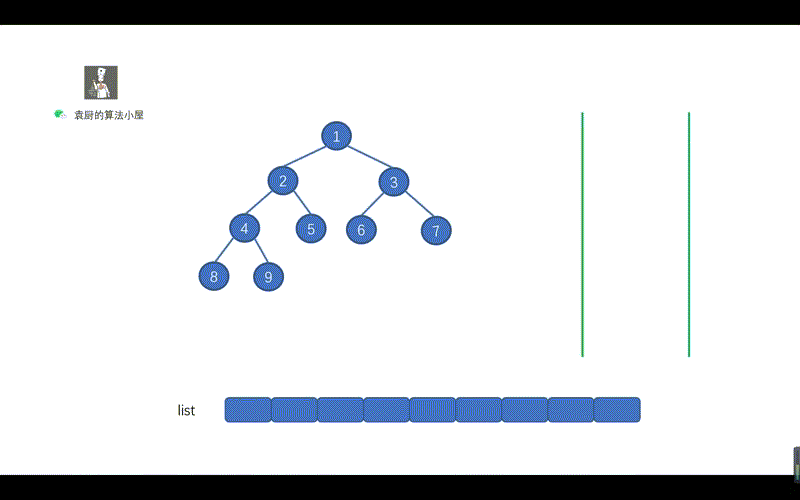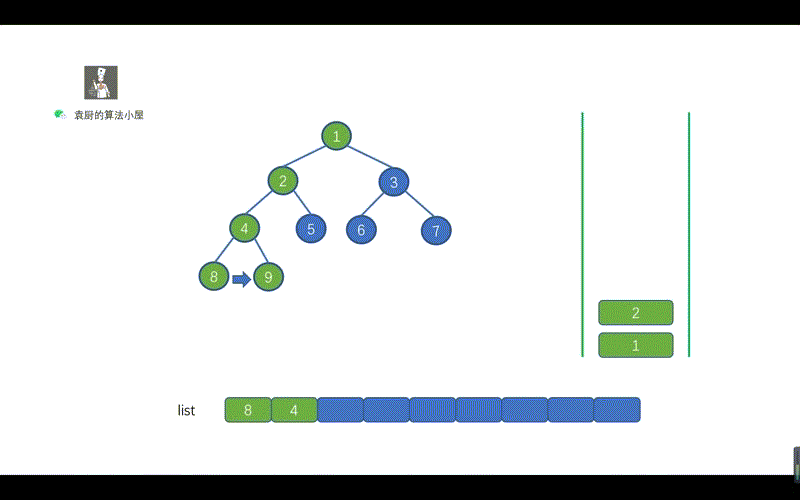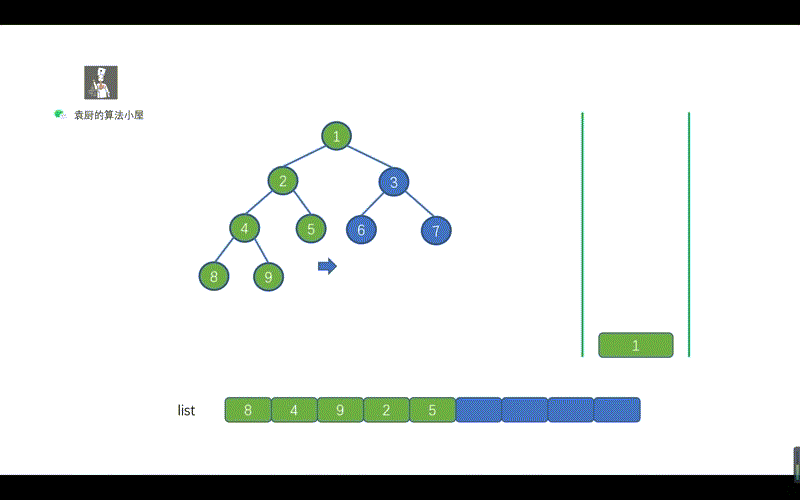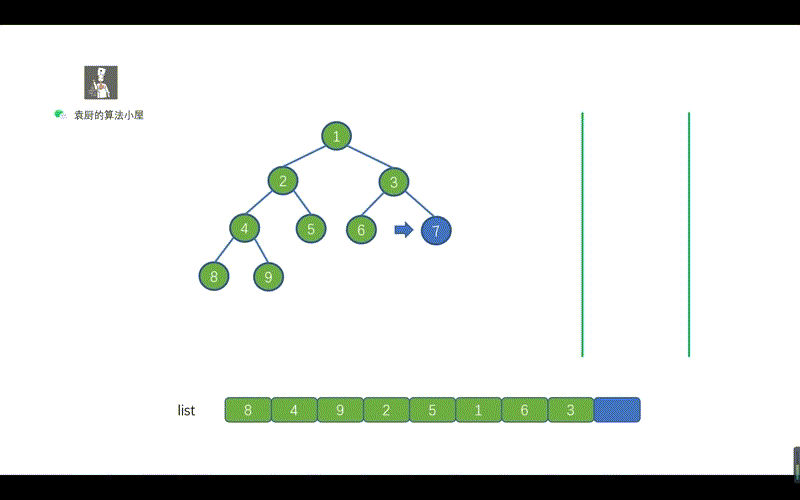
我们来看下面这个动画。
|
||
|
||
|
||
|
||
用栈实现的二叉树的中序遍历有两个关键的地方。
|
||
|
||
- 指针不断向节点的左孩子移动,为了找到我们当前需要遍历的节点。途中不断执行入栈操作
|
||
- 当指针为空时,则开始出栈,并将指针指向出栈节点的右孩子。
|
||
|
||
这两个关键点也很容易理解,指针不断向左孩子移动,是为了找到我们此时需要节点。然后当指针指向空时,则说明我们此时已经找到该节点,执行出栈操作,并将其值存入 list 即可,另外我们需要将指针指向出栈节点的右孩子,迭代执行上诉操作。
|
||
|
||
大家是不是已经知道怎么写啦,下面我们看代码吧。
|
||
|
||
```java
|
||
class Solution {
|
||
public List<Integer> inorderTraversal(TreeNode root) {
|
||
List<Integer> arr = new ArrayList<>();
|
||
TreeNode cur = new TreeNode(-1);
|
||
cur = root;
|
||
Stack<TreeNode> stack = new Stack<>();
|
||
while (!stack.isEmpty() || cur != null) {
|
||
//找到当前应该遍历的那个节点
|
||
while (cur != null) {
|
||
stack.push(cur);
|
||
cur = cur.left;
|
||
}
|
||
//此时指针指向空,也就是没有左子节点,则开始执行出栈操作
|
||
TreeNode temp = stack.pop();
|
||
arr.add(temp.val);
|
||
//指向右子节点
|
||
cur = temp.right;
|
||
}
|
||
return arr;
|
||
}
|
||
}
|
||
```
|
||
|
||
### **Morris**
|
||
|
||
我们之前说过,前序遍历的 Morris 方法,如果已经掌握,今天中序遍历的 Morris 方法也就没有什么难度,仅仅修改了一丢丢。
|
||
|
||
我们先来回顾一下前序遍历 Morris 方法的代码部分。
|
||
|
||
**前序遍历 Morris 代码**
|
||
|
||
```java
|
||
class Solution {
|
||
public List<Integer> preorderTraversal(TreeNode root) {
|
||
|
||
List<Integer> list = new ArrayList<>();
|
||
if (root == null) {
|
||
return list;
|
||
}
|
||
TreeNode p1 = root; TreeNode p2 = null;
|
||
while (p1 != null) {
|
||
p2 = p1.left;
|
||
if (p2 != null) {
|
||
//找到左子树的最右叶子节点
|
||
while (p2.right != null && p2.right != p1) {
|
||
p2 = p2.right;
|
||
}
|
||
//添加 right 指针,对应 right 指针为 null 的情况
|
||
//标注 1
|
||
if (p2.right == null) {
|
||
list.add(p1.val);
|
||
p2.right = p1;
|
||
p1 = p1.left;
|
||
continue;
|
||
}
|
||
//对应 right 指针存在的情况,则去掉 right 指针
|
||
p2.right = null;
|
||
//标注2
|
||
} else {
|
||
list.add(p1.val);
|
||
}
|
||
//移动 p1
|
||
p1 = p1.right;
|
||
}
|
||
return list;
|
||
}
|
||
}
|
||
```
|
||
|
||
我们先来看标注 1 的部分,这里的含义是,当找到 p1 指向节点的左子树中的最右子节点时。也就是下图中的情况,此时我们需要将 p1 指向的节点值,存入 list。
|
||
|
||
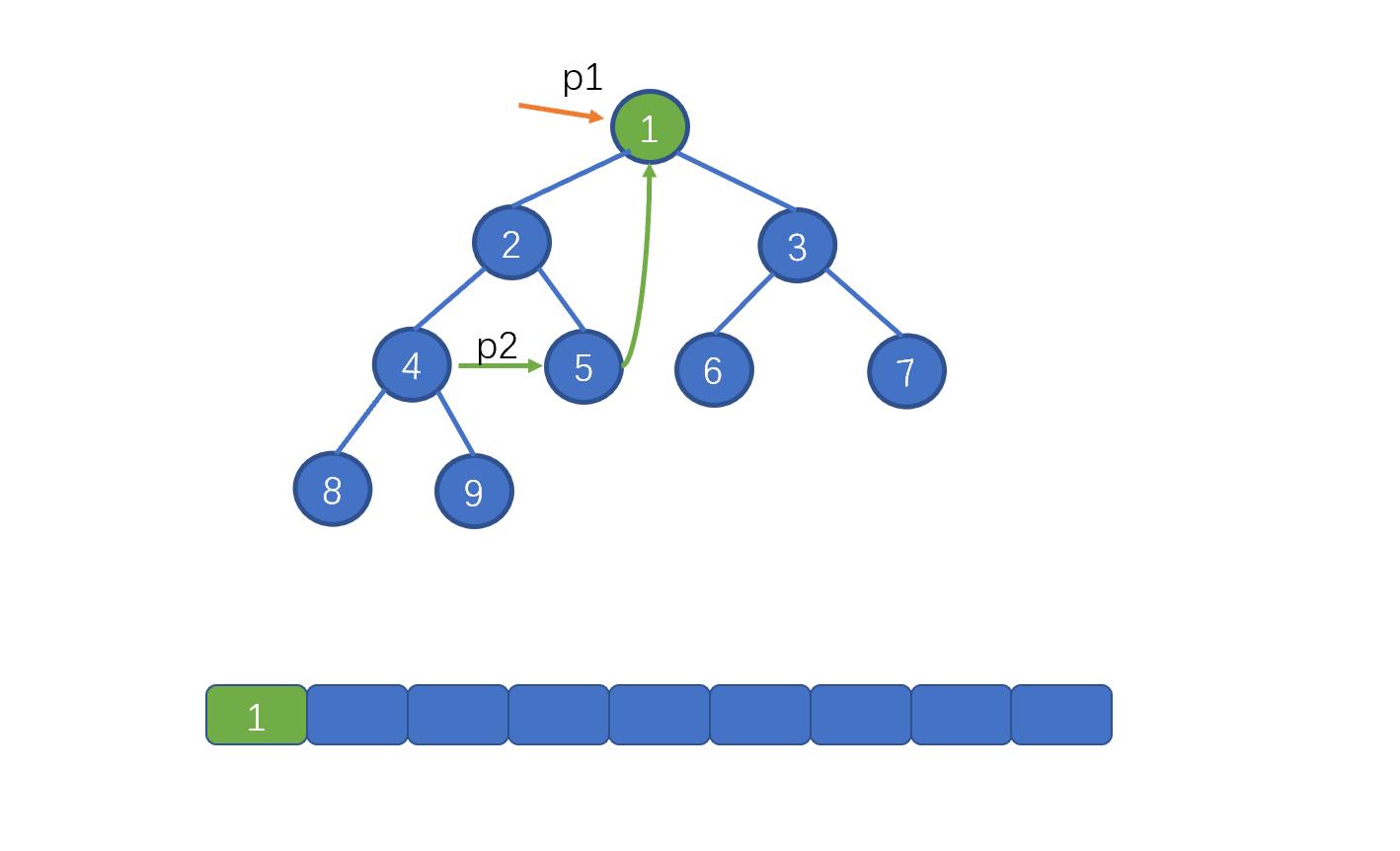
|
||
|
||
上述为前序遍历时的情况,那么中序遍历应该如何操作嘞。
|
||
|
||
前序遍历我们需要移动 p1 指针,`p1 = p1.left` 这样做的原因和上述迭代法原理一致,找到我们当前需要遍历的那个节点。
|
||
|
||
我们还需要修改哪里呢?见下图
|
||
|
||
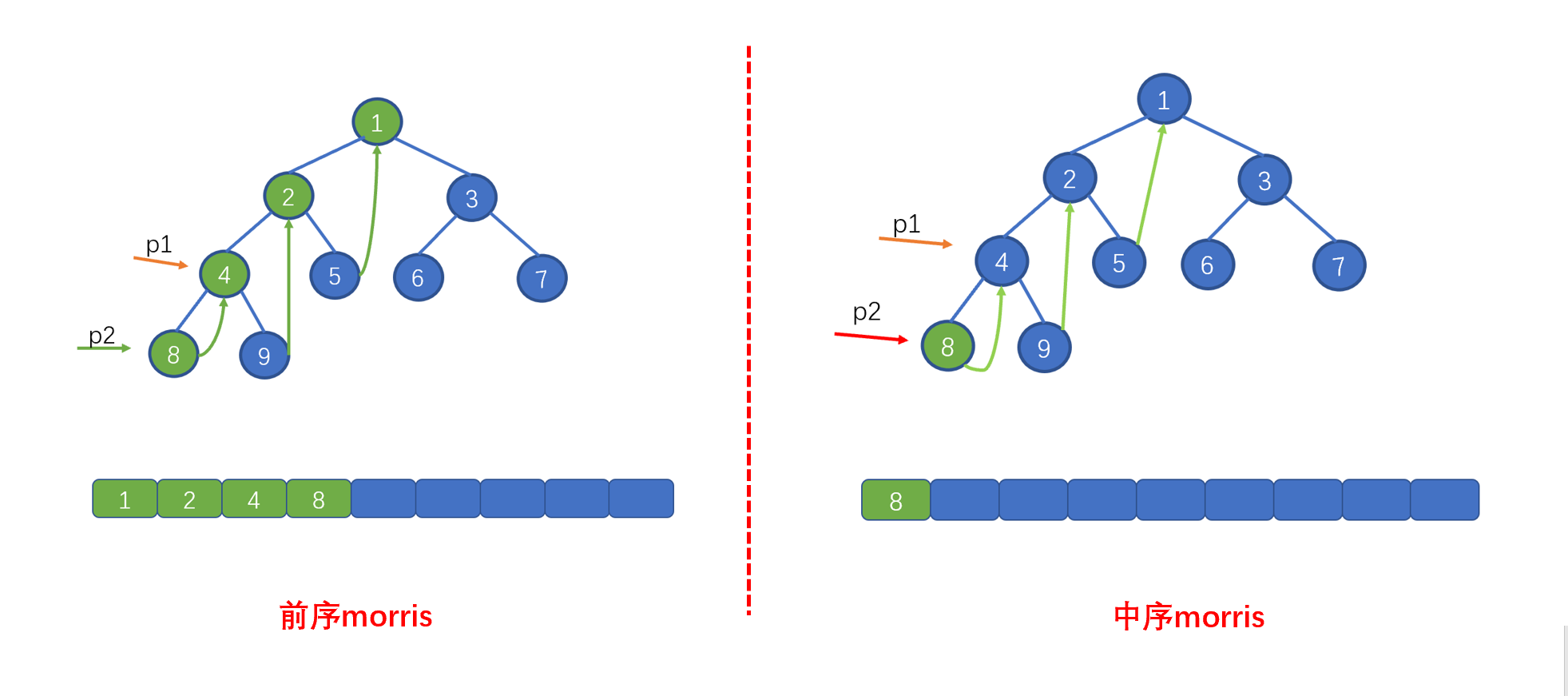
|
||
|
||
我们在前序遍历时,遇到 `p2.right == p1`的情况时,则会执行 `p2.right == null` 并让 `p1 = p1.right`,这样做是因为,我们此时 p1 指向的值已经遍历完毕,为了防止重复遍历。
|
||
|
||
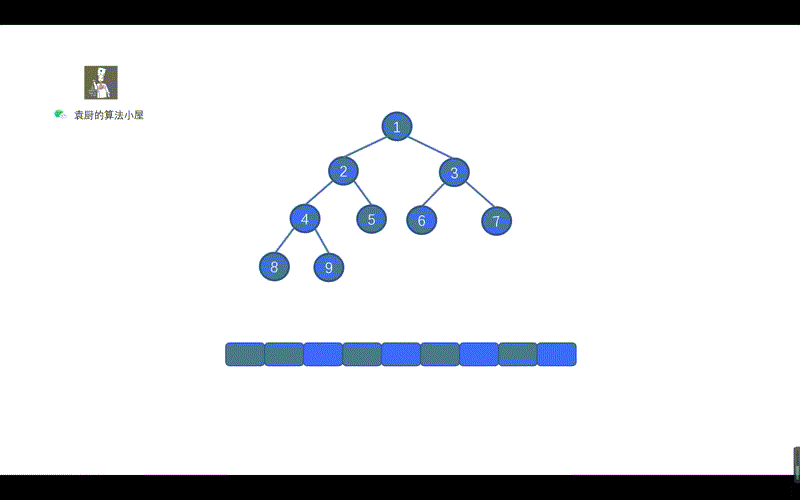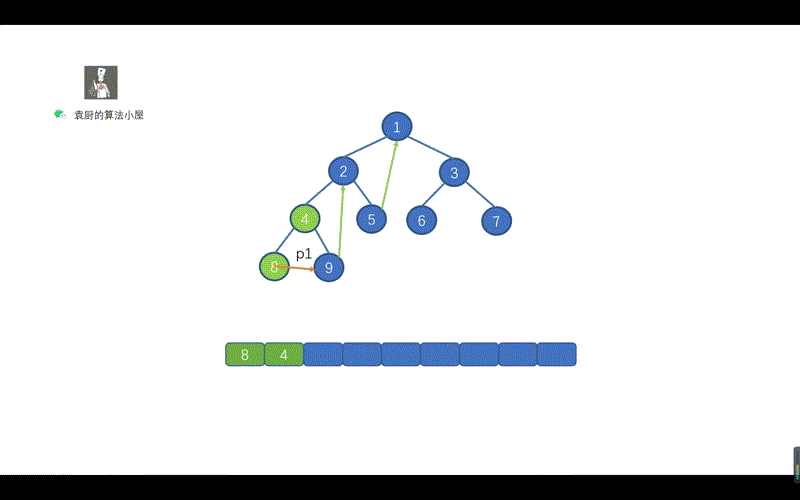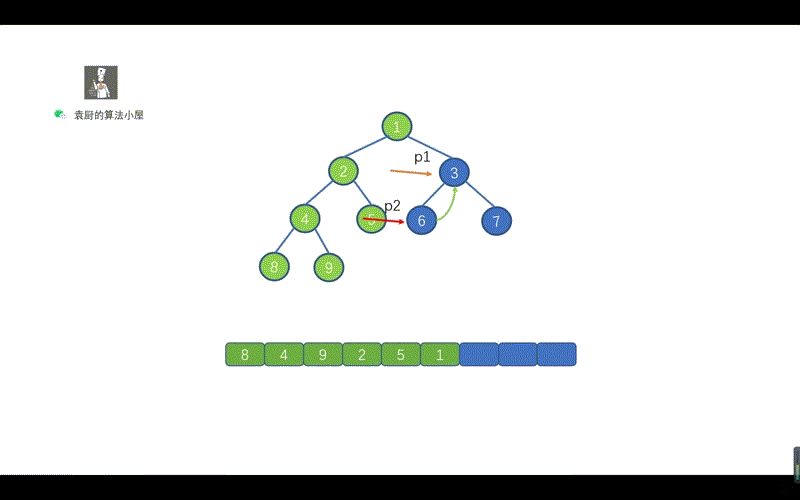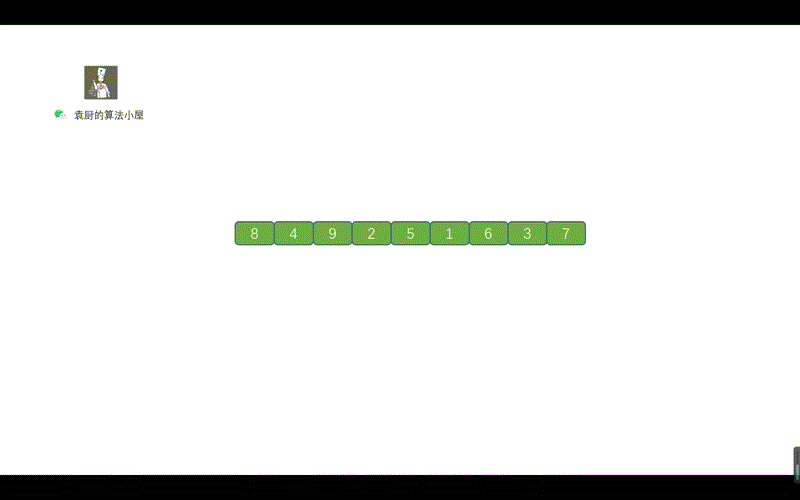
但是呢,在我们的中序 Morris 中我们遇到`p2.right == p1`此时 p1 还未遍历,所以我们需要在上面两条代码之间添加一行代码`list.add(p1.val);`
|
||
|
||
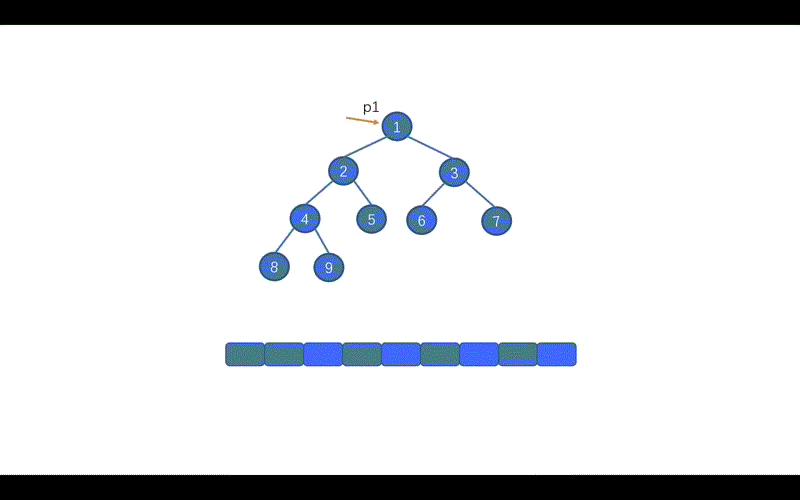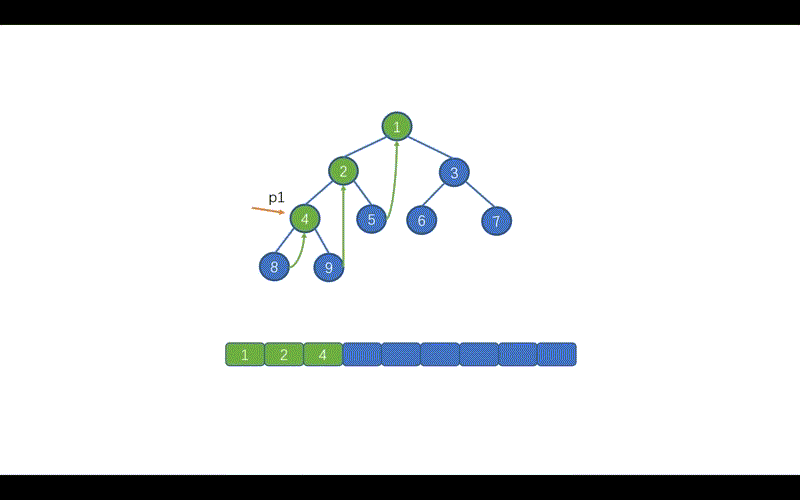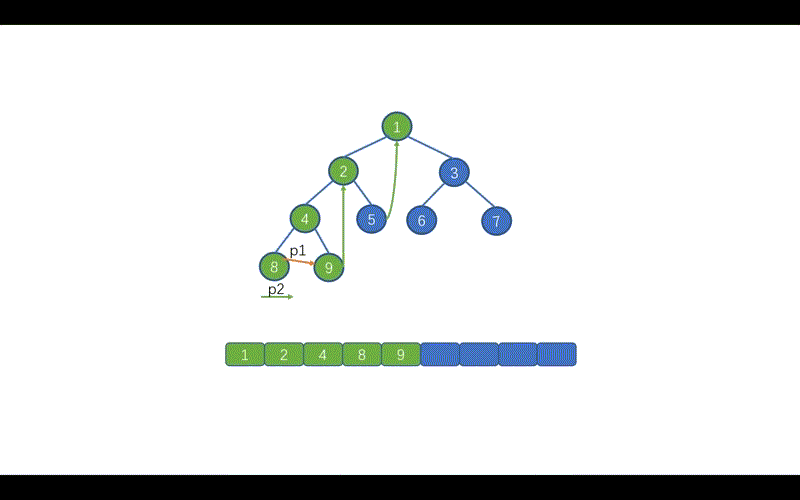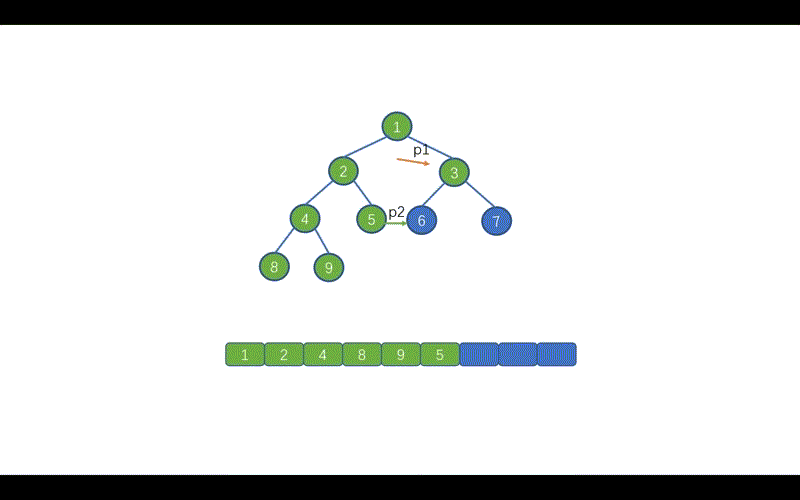
好啦,到这里我们就基本上就搞定了中序遍历的 Morris 方法,下面我们通过动画来加深一下印象吧,当然我也会把前序遍历的动画放在这里,大家可以看一下哪里有所不同。
|
||
|
||
|
||
|
||
|
||
|
||
|
||
|
||
**参考代码:**
|
||
|
||
```java
|
||
//中序 Morris
|
||
class Solution {
|
||
public List<Integer> inorderTraversal(TreeNode root) {
|
||
List<Integer> list = new ArrayList<Integer>();
|
||
if (root == null) {
|
||
return list;
|
||
}
|
||
TreeNode p1 = root;
|
||
TreeNode p2 = null;
|
||
while (p1 != null) {
|
||
p2 = p1.left;
|
||
if (p2 != null) {
|
||
while (p2.right != null && p2.right != p1) {
|
||
p2 = p2.right;
|
||
}
|
||
if (p2.right == null) {
|
||
p2.right = p1;
|
||
p1 = p1.left;
|
||
continue;
|
||
} else {
|
||
p2.right = null;
|
||
}
|
||
}
|
||
list.add(p1.val);
|
||
p1 = p1.right;
|
||
}
|
||
return list;
|
||
}
|
||
}
|
||
```
|
||
|